Question

第十八届省运会将于2014年9月在徐州市举办．为营造优美的环境，举办方决定在某“葫芦”形花坛中建喷泉．如图，该花坛的边界是两个半径为10米的圆弧围成，两圆心O₁、O₂之间的距离为10米．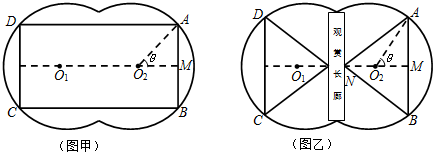
（1）如图甲，在花坛中建矩形喷泉，四个顶点A，B，C，D均在圆弧上，O₁O₂⊥AB于点M．设∠AO₂M=θ，求矩形的宽AB为多少时，可使喷泉ABCD的面积最大；
（2）如图乙，在花坛中间铺设一条宽为2米的观赏长廊以作休闲之用，则矩形喷泉变为两个全等的等腰三角形，其中NA=NB，NO₂=4米．若∠AO₂M=θ∈[

π

6

，

π

4

]，求喷泉的面积的取值范围．

Answer 1

考点：利用导数研究函数的单调性

专题：常规题型,应用题,导数的综合应用

分析：第（1）问要构造矩形的面积关于角θ的函数，需要利用三角函数把矩形的长和宽用角θ表示出来，进而利用矩形的面积公式表示面积，然后利用导数求函数的最值，在求解时要注意角θ的取值范围；
第（2）问由（1）容易得到喷泉面积关于角θ的函数，然后根据角θ的范围判断函数的单调性，进面求出面积的取值范围．

解答： 解：（1）在直角△AO₂M中，AM=10sinθ，O₂M=10cosθ，则AD=20cosθ+10，
所以矩形ABCD的面积S=20sinθ（20cosθ+10）=200（2sinθcosθ+sinθ），…（4分）
令f（θ）=2sinθcosθ+sinθ，0＜θ≤

π

3

，
则f'（θ）=2cos2θ+cosθ=4cos²θ+cosθ-2，
令f'（θ）=0，得cosθ=

33 -1

8

．设cosθ0=

33 -1

8

，且0＜θ0≤

π

3

，列表如下：

θ	（0，θ0）	θ0	(θ0， π 3 )
f'（θ）	+	0	-
f（θ）	↗	极大值	↘

所以当θ=θ₀，即AB=

5 30+2 33

2

时，矩形ABCD的面积最大．  …（10分）
（2）由（1）易得，喷泉的面积S=20sinθ（10cosθ+4）=100sin2θ+80sinθ，
由θ∈[

π

6

，

π

4

]知，2θ∈[

π

3

，

π

2

]，所以函数g（θ）=100sin2θ+80sinθ是单调增函数，
所以S∈[50

3

+40，100+40

2

]．                  …（13分）
答：（1）矩形的宽AB=

5 30+2 33

2

（米）时，可使喷泉ABCD的面积最大；
（2）喷泉的面积的取值范围是[50

3

+40，100+40

2

]（单位：平方米）．   …（14分）

点评：本题是一个应用题，关键是根据题意建立函数模型，在求最值时要特别注意变量角θ的取值范围．