题目内容
已知在数列{an}中，a1=2，a2=5，an=2an-1-an-2+4（n≥3）．
（1）求证：数列{an-an-1}（n≥2）是等差数列；
（2）求数列{an}的通项公式．
（1）求证：数列{an-an-1}（n≥2）是等差数列；
（2）求数列{an}的通项公式．
考点：等差数列的性质,数列递推式
专题：等差数列与等比数列
分析：（1）已知式子变形可得（an-an-1）-（an-1-an-2）=4，可得数列{an-an-1}是公差为4等差数列；
（2）进而可得数列{an-an-1}（n≥2）是公差为4，首项为3的等差数列，可得an-an-1=4n-1，累加法可得．
（2）进而可得数列{an-an-1}（n≥2）是公差为4，首项为3的等差数列，可得an-an-1=4n-1，累加法可得．
解答：
解：（1）∵当n≥3时，an=2an-1-an-2+4，
∴（an-an-1）-（an-1-an-2）=4
∴数列{an-an-1}（n≥2）是公差为4等差数列；
（2）∵a1=2，a2=5，∴a2-a1=5-2=3，
∴数列{an-an-1}（n≥2）是公差为4，首项为3的等差数列，
∴an-an-1=3+4（n-1）=4n-1，
∴a2-a1=7，a3-a2=11，…an-an-1=4n-1，
以上n-1个式子相加可得an-a1=
，
∴数列{an}的通项公式为an=2n2+n-1
∴（an-an-1）-（an-1-an-2）=4
∴数列{an-an-1}（n≥2）是公差为4等差数列；
（2）∵a1=2，a2=5，∴a2-a1=5-2=3，
∴数列{an-an-1}（n≥2）是公差为4，首项为3的等差数列，
∴an-an-1=3+4（n-1）=4n-1，
∴a2-a1=7，a3-a2=11，…an-an-1=4n-1，
以上n-1个式子相加可得an-a1=
| (n-1)(7+4n-1) |
| 2 |
∴数列{an}的通项公式为an=2n2+n-1
点评：本题考查等差数列的判定和数列的递推公式，属基础题．
练习册系列答案
相关题目
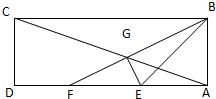在矩形ABCD中，AB=2，AD=6，E、F为AD的两个三等分点，AC和BF交于点G，△BEG的外接圆为圆H．
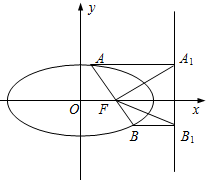已知点F为椭圆
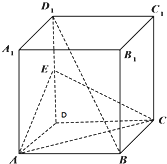如图，正方体ABCD-A1B1C1D1中，E为DD1的中点
在正三棱柱ABC-A1B1C1中，AB=2，AA1=3，点M，N在棱CC1，BB1上，且CM=B1N，则四棱锥A-BCMN的体积为