题目内容
已知{x,xy,lg(xy)}={0,|x|,y},求x,y的值.
考点:集合的相等
专题:集合
分析:结合对数函数的性质,得到xy=1,通过讨论\x|=1,y=1,从而得到x,y的值.
解答:
解:∵lg(xy) xy>0 x≠0且y≠0,
∴lg(xy)=0 xy=1,
A={x,1,0}={0,lxl,y},
若|x|=1 x=y,
x=1 y=1 A={1,1,0} 舍,
x=-1 y=-1,
A={-1,1,0},
若y=1 x=1 舍,
∴x=-1 y=-1.
∴lg(xy)=0 xy=1,
A={x,1,0}={0,lxl,y},
若|x|=1 x=y,
x=1 y=1 A={1,1,0} 舍,
x=-1 y=-1,
A={-1,1,0},
若y=1 x=1 舍,
∴x=-1 y=-1.
点评:本题考查了对数函数的性质,考查了集合的三要素,是一道基础题.

练习册系列答案
相关题目
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,根据收集到的数据(如下表),由最小二乘法求得回归直线方程
=0.68
+54.6,利用下表中数据推断a的值为( )
| ? |
| y |
| ? |
| x |
| 零件数x(个) | 10 | 20 | 30 | 40 | 50 |
| 加工时间y(min) | 62 | a | 75 | 81 | 89 |
| A、68.2 | B、68 |
| C、69 | D、67 |
如图,正方体ABCD-A1B1C1D1中,异面直线BC1和CD1所成角为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
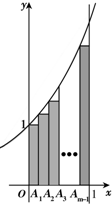 如图,A1,A2,…,Am-1(m≥2)为区间[0,1]上的m等分点,直线x=0,x=1,y=0和曲线y=ex所围成的区域为Ω1,图中m个矩形构成的阴影区域为Ω2,在Ω1中任取一点,则该点取自Ω2的概率等于
如图,A1,A2,…,Am-1(m≥2)为区间[0,1]上的m等分点,直线x=0,x=1,y=0和曲线y=ex所围成的区域为Ω1,图中m个矩形构成的阴影区域为Ω2,在Ω1中任取一点,则该点取自Ω2的概率等于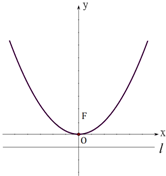 如图,抛物线C的顶点为坐标原点O,焦点F在y轴上,准线l与圆x2+y2=1相切.
如图,抛物线C的顶点为坐标原点O,焦点F在y轴上,准线l与圆x2+y2=1相切.