Question

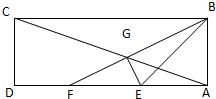在矩形ABCD中，AB=2，AD=6，E、F为AD的两个三等分点，AC和BF交于点G，△BEG的外接圆为圆H．
（1）求证：EG⊥BF；
（2）若圆H与圆C无公共点，求圆C半径的取值范围．

Answer 1

考点：直线和圆的方程的应用

专题：计算题,作图题,圆锥曲线的定义、性质与方程

分析：（1）在矩形ABCD中，以DA所在直线为x轴，以DA中点O为坐标原点，建立平面直角坐标系，可得A（3，0），B（3，2），C（-3，2），F（-1，0），从而可得G点的坐标为(

3

5

，

4

5

)，由kBF=

1

2

 ，kEG=-2证明EG⊥BF；
（2）写出圆H方程为 （x-2）²+（y-1）²=2，则由题意可得圆H内含于圆C或圆H与圆C相离，从而得CH＜r-

2

或CH＞r+

2

，从而求解．

解答： 解：（1）证明：在矩形ABCD中，以DA所在直线为x轴，以DA中点O为坐标原点，建立如图所示的平面直角坐标系． 

由题意可知A（3，0），B（3，2），C（-3，2），F（-1，0）．
所以直线AC和直线BF的方程分别为：x+3y-3=0，x-2y+1=0，
由

x+3y-3=0 x-2y+1=0

解得

x= 3 5 y= 4 5

，
所以G点的坐标为(

3

5

，

4

5

)．
所以kBF=

1

2

 ，kEG=-2，
因为k_BF•k_EG=-1，
所以EG⊥BF．
（2）由（1）知圆H的圆心为BE中点H（2，1），半径为BH=

2

，
所以圆H方程为 （x-2）²+（y-1）²=2．
圆C的圆心为C（-3，2），CH=

(-3-2)2+(2-1)2

=

26

，设的半径为r，（r＞0）
因为圆H与圆C无公共点，所以圆H内含于圆C或圆H与圆C相离，
故CH＜r-

2

或CH＞r+

2

所以0＜r＜

26

-

2

或r＞

26

+

2

，
即圆C半径的取值范围为(0，

26

-

2

)∪(

26

+

2

，+∞)．

点评：本题考查了线线垂直的判断与圆与圆的位置关系的应用，属于中档题．