题目内容
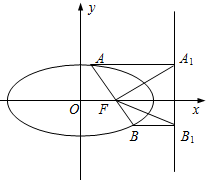 已知点F为椭圆
已知点F为椭圆| x2 |
| a2 |
| y2 |
| b2 |
(1)若点A为椭圆的上顶点,满足AF=2FB,且椭圆的右准线方程为x=3
| 3 |
(2)若点A,B在椭圆的右准线上的射影分别为A1,B1(如图所示),求证:∠A1FB1为锐角.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由题意可知,A(0,b),F(c,0),
=3
.设B(x0,y0),由已知条件推导出
=
.由此能求出椭圆的标准方程.
(2)设直线AB:x=my+c,设A1(
,y1),B1(
,y2),由
,得(a2+b2m2)y2+2mcb2y-b4=0,由此能推导出
•
=(
-c,y1)(
-c,y2)=
>0,从而得到∠A1FB1为锐角.
| a2 |
| c |
| 3 |
| c |
| a |
| ||
| 3 |
(2)设直线AB:x=my+c,设A1(
| a2 |
| c |
| a2 |
| c |
|
| FA1 |
| FB1 |
| a2 |
| c |
| a2 |
| c |
| b6(1+m2) |
| c2(a2+b2m2) |
解答:
(1)解:由题意可知,A(0,b),F(c,0),
=3
.…(1分)
设B(x0,y0),则
=(c,-b),
=(x0-c,y0),
因为AF=2FB,所以
=2
.…(3分)
即(c,-b)=(x0-c,y0)
所以
,解得
…(5分)
又因为点B在椭圆上,
所以
+
=1,解得
=
.
所以a=3,c=
,b=
.
因此椭圆的标准方程为
+
=1.…(7分)
(2)证明:设直线AB:x=my+c,(设斜率但不讨论不存在扣1分)…(9分)
设A1(
,y1),B1(
,y2),
由
,联立得(a2+b2m2)y2+2mcb2y-b4=0,
所以y1y2=-
,…(11分)
所以
•
=(
-c,y1)(
-c,y2)
=(
)2+y1y2
=
-
=
>0,…(14分)
又因为cos∠A1FB1=
>0,…(15分)
所以∠A1FB1为锐角. …(16分)
| a2 |
| c |
| 3 |
设B(x0,y0),则
| AF |
| FB |
因为AF=2FB,所以
| AF |
| FB |
即(c,-b)=(x0-c,y0)
所以
|
|
又因为点B在椭圆上,
所以
(
| ||
| a2 |
| ||
| b2 |
| c |
| a |
| ||
| 3 |
所以a=3,c=
| 3 |
| 6 |
因此椭圆的标准方程为
| x2 |
| 9 |
| y2 |
| 6 |
(2)证明:设直线AB:x=my+c,(设斜率但不讨论不存在扣1分)…(9分)
设A1(
| a2 |
| c |
| a2 |
| c |
由
|
所以y1y2=-
| b4 |
| a2+b2m2 |
所以
| FA1 |
| FB1 |
| a2 |
| c |
| a2 |
| c |
=(
| b2 |
| c |
=
| b4 |
| c2 |
| b4 |
| a2+b2m2 |
=
| b6(1+m2) |
| c2(a2+b2m2) |
又因为cos∠A1FB1=
| FA1•FB1 |
| |FA1|•|FB1| |
所以∠A1FB1为锐角. …(16分)
点评:本题考查椭圆方程的求法,考查角为锐角的证明,解题时要认真审题,注意函数与方程思想的合理运用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
若函数f(x)=|ax+x2-x•lna-m|-2,(a>0且a≠1)有两个零点,则m的取值范围( )
| A、(-1,3) |
| B、(-3,1) |
| C、(3,+∞) |
| D、(-∞,-1) |
△ABC的内角A、B、C对边的长a、b、c成等比数列,则
的取值范围是( )
| sinB+sinC |
| sinA |
| A、(0,+∞) | ||
B、(0,2+
| ||
| C、(1,+∞) | ||
D、(1,2+
|