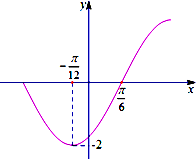
题目内容
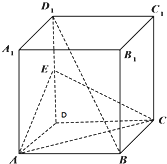 如图,正方体ABCD-A1B1C1D1中,E为DD1的中点
如图,正方体ABCD-A1B1C1D1中,E为DD1的中点(Ⅰ)求证:直线BD1⊥AC;
(Ⅱ)求异面直线BD1与CE所成角的余弦值.
考点:异面直线及其所成的角,空间中直线与直线之间的位置关系
专题:空间位置关系与距离,空间角
分析:(I)证明AC⊥BD,且AC⊥DD1,即可证明AC⊥平面BDD1,从而证明AC⊥BD1;
(Ⅱ)在平面ABB1A1作BF∥CE,得到∠FBD1为异面直线BD1与CE所成角,借助于余弦定理求其余弦值.
(Ⅱ)在平面ABB1A1作BF∥CE,得到∠FBD1为异面直线BD1与CE所成角,借助于余弦定理求其余弦值.
解答:
 (I)证明:在正方体ABCD中,连结BD,
(I)证明:在正方体ABCD中,连结BD,
∴AC⊥BD,
又∵DD1⊥平面ABCD,且AC?平面ABCD,
∴AC⊥DD1,
∴AC⊥平面BDD1,
∵BD1?平面BDD1,
∴直线BD1⊥AC;
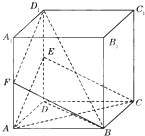
(Ⅱ)解:在平面ABB1A1作BF∥CE,
则∠FBD1为异面直线BD1与CE所成角,
连接FD1,如图,
设正方体棱长为2,则BF2=5,FD12=5,BD12=12,
∴cos∠FBD1=
=
=-
,
∴异面直线BD1与CE所成角的余弦值
;
 (I)证明:在正方体ABCD中,连结BD,
(I)证明:在正方体ABCD中,连结BD,∴AC⊥BD,
又∵DD1⊥平面ABCD,且AC?平面ABCD,
∴AC⊥DD1,
∴AC⊥平面BDD1,
∵BD1?平面BDD1,
∴直线BD1⊥AC;
(Ⅱ)解:在平面ABB1A1作BF∥CE,
则∠FBD1为异面直线BD1与CE所成角,
连接FD1,如图,
设正方体棱长为2,则BF2=5,FD12=5,BD12=12,
∴cos∠FBD1=
| BF2+BD12-FD12 |
| 2×BF×BD1 |
| 5+5-12 |
| 2×5 |
| 1 |
| 5 |
∴异面直线BD1与CE所成角的余弦值
| 1 |
| 5 |
点评:本题考查了正方体中的线线关系;关键是熟练正方体的性质以及线面垂直的判定定理.

练习册系列答案
相关题目
如图,正方体ABCD-A1B1C1D1中,异面直线BC1和CD1所成角为( )


A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=
,点O为坐标原点,点An(n,f(n))(n∈N*).若记直线OAn的倾斜角为θn,则tanθ1+tanθ2+…+tanθn=( )
| 1 |
| x+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|