题目内容
如图，已知AB是圆O的直径，C是AB延长线上一点，CD切圆O于D，CD=4，AB=3BC，则圆O的半径长是考点：与圆有关的比例线段
专题：直线与圆
分析：利用切割线定理即可得出．
解答：
解：设圆的半径为r，∵AB=3BC，∴2r=3BC．
∵CD切圆O于D，∴CD2=CB•CA，∴42=
•(
+2r)，化为r2=9，解得r=3．
故答案为：3．
∵CD切圆O于D，∴CD2=CB•CA，∴42=
| 2r |
| 3 |
| 2r |
| 3 |
故答案为：3．
点评：本题考查了切割线定理，属于基础题．
练习册系列答案
53随堂测系列答案
相关题目
已知O是坐标原点，点A（2，0），△AOC的顶点C在曲线y2=4（x-1）上，那么△AOC的重心G的轨迹方程是（ ）
| A、3y2=4（x-1） | ||
| B、3y2=4（x-1）（y≠0） | ||
C、
| ||
D、
|
已知点P（x，y）满足x2+y2-2y=0，则u=
的取值范围是（ ）
| y+1 |
| x |
A、-
| ||||||||
B、μ≤-
| ||||||||
C、-
| ||||||||
D、μ≤-
|
（坐标系与参数方程选做题）如图所示的极坐标系中，以M（4，函数g（x）=lnx-
的零点所在区间是（ ）
| 1 |
| x |
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |
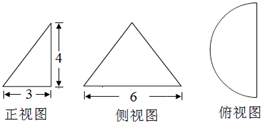某几何体的三视图如图所示（单位：cm），则其体积和表面积分别是（ ）| A、6πcm3和12（1+π）cm2 |
| B、6πcm3和12πcm2 |
| C、12πcm3和12（1+π）cm2 |
| D、12πcm3和12πcm2 |