题目内容
已知向量
=(cos75°,sin75°),
=(cos15°,sin15°),那么|
+2
|的值为( )
| a |
| b |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
| D、3 |
考点:平面向量数量积的坐标表示、模、夹角
专题:平面向量及应用
分析:利用向量的模的计算公式、数量积的运算及其性质即可得出.
解答:
解:∵向量
=(cos75°,sin75°),
=(cos15°,sin15°),
∴|
|=
=1,|
|=
=1,
•
=cos75°cos15°+sin75°sin15°=cos(75°-15°)=cos60°=
.
∴|
+2
|=
=
=
.
故选:C.
| a |
| b |
∴|
| a |
| cos275°+sin275° |
| b |
| cos215°+sin215° |
| a |
| b |
| 1 |
| 2 |
∴|
| a |
| b |
|
12+4×12+4×
|
| 7 |
故选:C.
点评:本题考查了向量的模的计算公式、数量积的运算及其性质,属于基础题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
曲线
+
=1的焦点坐标为( )
| y2 |
| 16 |
| x2 |
| 9 |
A、(0,±
| ||
B、(±
| ||
| C、(0,±5) | ||
| D、(±5,0) |
设某种产品分两道工序生产,第一道工序的次品率为10%,第二道工序的次品率为3%.生产这种产品只要有一道工序出次品就出次品,则该产品的次品率是( )
| A、0.13 | B、0.03 |
| C、0.127 | D、0.873 |
两球的体积之比为8:1,则它们的表面积之比为( )
| A、8:1 | ||
| B、4:1 | ||
C、2
| ||
| D、2:1 |
若数列{an}的前n项和Sn满足Sn=4-an(n∈N*),则a5=( )
| A、1 | ||
B、
| ||
C、
| ||
D、
|
某少数民族的刺绣有着悠久的历史,如图所示(1)(2)(3)(4)为她们刺绣最简单的四个图案,这些图案都由小正方形构成,小正方形数越多刺绣越漂亮,现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.则f(5)等于( )


| A、39 | B、40 | C、41 | D、42 |
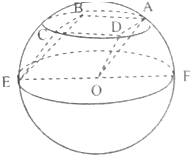 如图,三棱柱OAD-EBC,其中A,B,C,D,E均在以O为球心,半径为2的球面上,EF为直径,侧面ABCD为边长等于2的正方形,则三棱柱OAD-EBC的体积为( )
如图,三棱柱OAD-EBC,其中A,B,C,D,E均在以O为球心,半径为2的球面上,EF为直径,侧面ABCD为边长等于2的正方形,则三棱柱OAD-EBC的体积为( )