题目内容
16.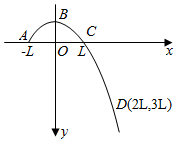 从A点斜向上抛出一个小球,曲线ABCD是小球运动的一段轨迹,建立如图所示的正交坐标系xOy,x轴沿水平方向,轨迹上三个点的坐标分别为A(-L,0),C(L,0),D(2L,3L),小球受到的空气阻力忽略不计,轨迹与y轴的交点B的坐标为( )
从A点斜向上抛出一个小球,曲线ABCD是小球运动的一段轨迹,建立如图所示的正交坐标系xOy,x轴沿水平方向,轨迹上三个点的坐标分别为A(-L,0),C(L,0),D(2L,3L),小球受到的空气阻力忽略不计,轨迹与y轴的交点B的坐标为( )| A. | (0,-$\frac{L}{2}$) | B. | (0,-L) | C. | (0,-$\frac{3L}{2}$) | D. | (0,-2L) |
分析 由函数图象可知,轨迹为二次函数,开口向下且过点(-L,0)和(L,0),设函数解析式y=-a(x-L)(x+L),将(2L,3L)代入方程求出解析式,再将x=0代入,即求得B的纵坐标.
解答 解:由函数图象可知,轨迹为二次函数,过点(-L,0)和(L,0),设函数解析式y=-a(x-L)(x+L)
将(2L,3L)代入方程,解得a=-$\frac{1}{L}$
y=$\frac{1}{L}$(x-L)(x+L),将x=0代入得y=-L
故答案选B
点评 本题主要考察二次函数解析,属于基础题.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
6.设$\overrightarrow{a}$,$\overrightarrow{b}$是两个非零向量,若命题p:$\overrightarrow{a}$•$\overrightarrow{b}$>0,命题q:$\overrightarrow{a}$,$\overrightarrow{b}$夹角是锐角,则命题p是命题q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
1.已知cos(α+$\frac{π}{2}$)=$\frac{3}{5}$,-$\frac{π}{2}$<α<$\frac{π}{2}$,则sin2α的值等于( )
| A. | $\frac{12}{25}$ | B. | -$\frac{12}{25}$ | C. | $\frac{24}{25}$ | D. | -$\frac{24}{25}$ |