题目内容
1．已知cos（α+$\frac{π}{2}$）=$\frac{3}{5}$，-$\frac{π}{2}$＜α＜$\frac{π}{2}$，则sin2α的值等于（ ）| A． | $\frac{12}{25}$ | B． | -$\frac{12}{25}$ | C． | $\frac{24}{25}$ | D． | -$\frac{24}{25}$ |
分析 由题意和诱导公式可得sinα，由同角三角函数基本关系可得cosα，代入二倍角的正弦公式可得．
解答 解：∵cos（α+$\frac{π}{2}$）=$\frac{3}{5}$，∴-sinα=$\frac{3}{5}$，即sinα=-$\frac{3}{5}$，
又∵-$\frac{π}{2}$＜α＜$\frac{π}{2}$，∴cosα=$\sqrt{1-si{n}^{2}α}$=$\frac{4}{5}$，
∴sin2α=2sinαcosα=2×（-$\frac{3}{5}$）×$\frac{4}{5}$=-$\frac{24}{25}$，
故选：D．
点评 本题考查二倍角的正弦公式，涉及同角三角函数基本关系，属基础题．
练习册系列答案
相关题目
11．齐王与田忌赛马，田忌的上等马优于齐王的中等马，劣于齐王的上等马，田忌的中等马优于齐王的下等马，劣于齐王的中等马，田忌的下等马劣于齐王的下等马，现从双方的马匹中随机选一匹马进行一场比赛，则田忌获胜的概率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{5}$ | D． | $\frac{1}{6}$ |
12．若sinα=$\frac{3}{5}$，则tanα的值等于（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{3}{4}$ | C． | $-\frac{3}{4}$ | D． | $±\frac{3}{4}$ |
16．
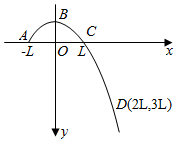从A点斜向上抛出一个小球，曲线ABCD是小球运动的一段轨迹，建立如图所示的正交坐标系xOy，x轴沿水平方向，轨迹上三个点的坐标分别为A（-L，0），C（L，0），D（2L，3L），小球受到的空气阻力忽略不计，轨迹与y轴的交点B的坐标为（ ）
从A点斜向上抛出一个小球，曲线ABCD是小球运动的一段轨迹，建立如图所示的正交坐标系xOy，x轴沿水平方向，轨迹上三个点的坐标分别为A（-L，0），C（L，0），D（2L，3L），小球受到的空气阻力忽略不计，轨迹与y轴的交点B的坐标为（ ）| A． | （0，-$\frac{L}{2}$） | B． | （0，-L） | C． | （0，-$\frac{3L}{2}$） | D． | （0，-2L） |