题目内容
8.记z=x+ky+1,(k∈R),其中x,y满足$\left\{\begin{array}{l}{2x-y-2≤0}\\{x-2y+2≥0}\\{x+y-1≥0}\end{array}\right.$,若z的最大值为3,则实数k的值为0,z的最小值为1.分析 作出可行域,根据z的最大值为3,判断目标函数的斜率得出k的值,根据可行域得出最优解的位置,计算z的最小值.
解答 解:作出约束条件的可行域,如图所示: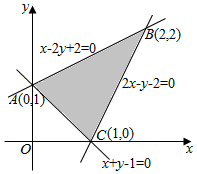
(1)若k=0,则z=x+1,显然当x=2时z取得最大值3,符合题意,此时,当x=0时,z取得最小值1.
(2)若k≠0,由z=x+ky+1得y=-$\frac{1}{k}x+\frac{z-1}{k}$.
①若k>0,则当直线y=-$\frac{1}{k}x+\frac{z-1}{k}$经过点B(2,2)时,直线截距最大,即z最大.
∴3=2+2k+1,解得k=0(舍),
②若k<0,则当-$\frac{1}{k}$≤2即k≤-$\frac{1}{2}$时,直线y=-$\frac{1}{k}x+\frac{z-1}{k}$经过点C(1,0)时,直线截距最小,即z最大.
∴3=1+0×k+1,无解.
当-$\frac{1}{k}$≥2即-$\frac{1}{2}≤$k<0时,直线y=-$\frac{1}{k}x+\frac{z-1}{k}$经过点B(2,2)时,直线截距最小,即z最大
∴3=2+2k+1,解得k=0(舍).
综上,k=0,z的最小值为1.
故答案为0,1.
点评 本题考查了简单的线性规划,根据可行域判断最优解的位置是解题关键,属于中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
18.已知命题¬p:存在x∈(1,2)使得ex-a>0,若p是真命题,则实数a的取值范围为( )
| A. | (-∞,e) | B. | (-∞,e] | C. | (e2,+∞) | D. | [e2,+∞) |
16.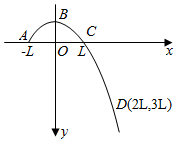 从A点斜向上抛出一个小球,曲线ABCD是小球运动的一段轨迹,建立如图所示的正交坐标系xOy,x轴沿水平方向,轨迹上三个点的坐标分别为A(-L,0),C(L,0),D(2L,3L),小球受到的空气阻力忽略不计,轨迹与y轴的交点B的坐标为( )
从A点斜向上抛出一个小球,曲线ABCD是小球运动的一段轨迹,建立如图所示的正交坐标系xOy,x轴沿水平方向,轨迹上三个点的坐标分别为A(-L,0),C(L,0),D(2L,3L),小球受到的空气阻力忽略不计,轨迹与y轴的交点B的坐标为( )
 从A点斜向上抛出一个小球,曲线ABCD是小球运动的一段轨迹,建立如图所示的正交坐标系xOy,x轴沿水平方向,轨迹上三个点的坐标分别为A(-L,0),C(L,0),D(2L,3L),小球受到的空气阻力忽略不计,轨迹与y轴的交点B的坐标为( )
从A点斜向上抛出一个小球,曲线ABCD是小球运动的一段轨迹,建立如图所示的正交坐标系xOy,x轴沿水平方向,轨迹上三个点的坐标分别为A(-L,0),C(L,0),D(2L,3L),小球受到的空气阻力忽略不计,轨迹与y轴的交点B的坐标为( )| A. | (0,-$\frac{L}{2}$) | B. | (0,-L) | C. | (0,-$\frac{3L}{2}$) | D. | (0,-2L) |