题目内容
5.已知函数f(x)=$\sqrt{{x}^{2}+1}$-ax(其中a>0)在区间[0,+∞)上是单调函数,则实数a的取值范围为[1,+∞).分析 求导数便可得到$f′(x)=\frac{x}{\sqrt{{x}^{2}+1}}-a$,从而x∈[0,+∞)便有$\frac{x}{\sqrt{{x}^{2}+1}}≥0$,这样根据f(x)在[0,+∞)上是单调函数便可得出a≤0,即得出了实数a的取值范围.
解答 解:$f′(x)=\frac{x}{\sqrt{{x}^{2}+1}}-a$;
∵f(x)在区间[0,+∞)上是单调函数,且x∈[0,+∞)时,$\frac{x}{\sqrt{{x}^{2}+1}}=\frac{1}{\sqrt{1+\frac{1}{{x}^{2}}}}$;
∴$0≤\frac{x}{\sqrt{{x}^{2}+1}}<1$;
又a>0;
∴a≥1;
∴a的取值范围为[1,+∞).
故答案为:[1,+∞).
点评 考查函数单调性和函数导数符号的关系,以及复合函数的求导公式,注意正确求导.

练习册系列答案
相关题目
16.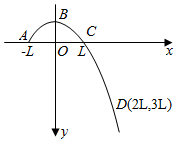 从A点斜向上抛出一个小球,曲线ABCD是小球运动的一段轨迹,建立如图所示的正交坐标系xOy,x轴沿水平方向,轨迹上三个点的坐标分别为A(-L,0),C(L,0),D(2L,3L),小球受到的空气阻力忽略不计,轨迹与y轴的交点B的坐标为( )
从A点斜向上抛出一个小球,曲线ABCD是小球运动的一段轨迹,建立如图所示的正交坐标系xOy,x轴沿水平方向,轨迹上三个点的坐标分别为A(-L,0),C(L,0),D(2L,3L),小球受到的空气阻力忽略不计,轨迹与y轴的交点B的坐标为( )
 从A点斜向上抛出一个小球,曲线ABCD是小球运动的一段轨迹,建立如图所示的正交坐标系xOy,x轴沿水平方向,轨迹上三个点的坐标分别为A(-L,0),C(L,0),D(2L,3L),小球受到的空气阻力忽略不计,轨迹与y轴的交点B的坐标为( )
从A点斜向上抛出一个小球,曲线ABCD是小球运动的一段轨迹,建立如图所示的正交坐标系xOy,x轴沿水平方向,轨迹上三个点的坐标分别为A(-L,0),C(L,0),D(2L,3L),小球受到的空气阻力忽略不计,轨迹与y轴的交点B的坐标为( )| A. | (0,-$\frac{L}{2}$) | B. | (0,-L) | C. | (0,-$\frac{3L}{2}$) | D. | (0,-2L) |
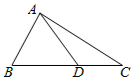 如图,在△ABC中,角A,B,C所对的边分别为a,b,c,sinA=$\frac{1}{4}$acosB,b=4$\sqrt{3}$.
如图,在△ABC中,角A,B,C所对的边分别为a,b,c,sinA=$\frac{1}{4}$acosB,b=4$\sqrt{3}$.