题目内容
7.已知随机变量ξ服从正态分布N(2,σ2),若P(X<a)=0.28,则P(a≤X≤4-a)=0.44.分析 根据随机变量X服从正态分布N(2,σ2),看出这组数据对应的正态曲线的对称轴x=2,根据正态曲线的特点,得到P(a≤X≤4-a)=1-2P(X<a),得到结果.
解答 解:∵随机变量X服从正态分布N(2,σ2),
对称轴是:x=2,
又4-a与a关于x=2对称,由正态曲线的对称性得:
∴P(a≤X≤4-a)=1-2P(X<a))=1-2×0.28=0.44.
故答案为:0.44.
点评 本题考查正态分布,正态曲线的特点,若一个随机变量如果是众多的、互不相干的、不分主次的偶然因素作用结果之和,它就服从或近似的服从正态分布.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
17.执行如图的程序框图,若输入?=0.01,则输出的N=( )


| A. | 102 | B. | 101 | C. | 100 | D. | 99 |
18.已知命题¬p:存在x∈(1,2)使得ex-a>0,若p是真命题,则实数a的取值范围为( )
| A. | (-∞,e) | B. | (-∞,e] | C. | (e2,+∞) | D. | [e2,+∞) |
12.若sinα=$\frac{3}{5}$,则tanα的值等于( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{4}$ | C. | $-\frac{3}{4}$ | D. | $±\frac{3}{4}$ |
16.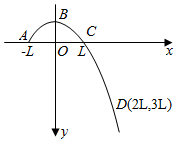 从A点斜向上抛出一个小球,曲线ABCD是小球运动的一段轨迹,建立如图所示的正交坐标系xOy,x轴沿水平方向,轨迹上三个点的坐标分别为A(-L,0),C(L,0),D(2L,3L),小球受到的空气阻力忽略不计,轨迹与y轴的交点B的坐标为( )
从A点斜向上抛出一个小球,曲线ABCD是小球运动的一段轨迹,建立如图所示的正交坐标系xOy,x轴沿水平方向,轨迹上三个点的坐标分别为A(-L,0),C(L,0),D(2L,3L),小球受到的空气阻力忽略不计,轨迹与y轴的交点B的坐标为( )
 从A点斜向上抛出一个小球,曲线ABCD是小球运动的一段轨迹,建立如图所示的正交坐标系xOy,x轴沿水平方向,轨迹上三个点的坐标分别为A(-L,0),C(L,0),D(2L,3L),小球受到的空气阻力忽略不计,轨迹与y轴的交点B的坐标为( )
从A点斜向上抛出一个小球,曲线ABCD是小球运动的一段轨迹,建立如图所示的正交坐标系xOy,x轴沿水平方向,轨迹上三个点的坐标分别为A(-L,0),C(L,0),D(2L,3L),小球受到的空气阻力忽略不计,轨迹与y轴的交点B的坐标为( )| A. | (0,-$\frac{L}{2}$) | B. | (0,-L) | C. | (0,-$\frac{3L}{2}$) | D. | (0,-2L) |