题目内容
4.下列关于概率和统计的几种说法:①10名工人某天生产同一种零件,产生的件数分别是15,17,14,10,15,17,17,16,14,12,设其平均数为a,中位数为b,众数为c,则a,b,c的大小为c>a>b;②样本4,2,1,0,-2的标准差是2;③在面积为S的△ABC内任选一点P,则随机事件“△PBC的面积小于$\frac{S}{3}$”的概率为$\frac{1}{3}$;④从写有0,1,2,…,9的十张卡片中,有放回地每次抽一张,连抽两次,则两张卡片上的数字各不相同的概率为$\frac{9}{10}$.其中正确说法的序号有④.分析 ①根据平均数,中位数,众数的定义进行比较即可.
②根据标准差的公式进行判断.
③根据几何概型的概率公式进行求解判断.
④根据概率公式进行判断.
解答 解::①10名工人某天生产同一种零件,产生的件数分别是15,17,14,10,15,17,17,16,14,12,
安装大小排列为10,12,14,14,15,15,16,17,17,17,则其平均数为a=15+$\frac{1}{10}$(-5-3-1-1+1+2+2+2)=15-0.3=14.7,
中位数为b=15,众数为c=17,则a,b,c的大小为c>b>a;故①错误,
②样本4,2,1,0,-2的平均数为1,标准差$\frac{1}{5}$$\sqrt{(4-1)^{2}+(2-1)^{2}+(0-1)^{2}+(-2-1)^{2}}$=$\frac{1}{5}$$•\sqrt{20}$=$\frac{2\sqrt{5}}{5}$,故②错误;
③解:作出△ABC的高AO,当“△PBC的面积等于$\frac{S}{3}$”时,此时OP=$\frac{1}{3}AO$,
要使“△PBC的面积小于$\frac{S}{3}$”,则P位于阴影部分,
则△AEF的面积S1=$(\frac{2}{3})^{2}S=\frac{4}{9}S$,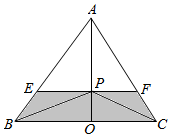
则阴影部分的面积为$S-\frac{4}{9}S=\frac{5}{9}S$,
则根据几何概型的概率公式可得“△PBC的面积小于$\frac{S}{3}$”的概率为$\frac{\frac{5}{9}S}{S}=\frac{5}{9}$,故③错误,
④由题意知本题是一个等可能事件的概率,
试验发生所包含的事件数是10×10=100,
满足条件的事件数,第一次有10种结果,第二次有9种结果,共有10×9=90种结果,
∴两张卡片数字各不相同的概率是P=$\frac{90}{100}$=$\frac{9}{10}$.故④正确,
故答案为:④
点评 本题主要考查命题的真假判断,涉及统计与概率的知识,综合性较强,有一定的难度.

| A. | $\frac{4}{5}$ | B. | $\frac{3}{4}$ | C. | $-\frac{3}{4}$ | D. | $±\frac{3}{4}$ |
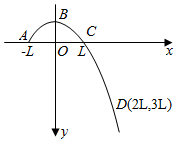 从A点斜向上抛出一个小球,曲线ABCD是小球运动的一段轨迹,建立如图所示的正交坐标系xOy,x轴沿水平方向,轨迹上三个点的坐标分别为A(-L,0),C(L,0),D(2L,3L),小球受到的空气阻力忽略不计,轨迹与y轴的交点B的坐标为( )
从A点斜向上抛出一个小球,曲线ABCD是小球运动的一段轨迹,建立如图所示的正交坐标系xOy,x轴沿水平方向,轨迹上三个点的坐标分别为A(-L,0),C(L,0),D(2L,3L),小球受到的空气阻力忽略不计,轨迹与y轴的交点B的坐标为( )| A. | (0,-$\frac{L}{2}$) | B. | (0,-L) | C. | (0,-$\frac{3L}{2}$) | D. | (0,-2L) |
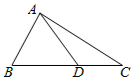 如图,在△ABC中,角A,B,C所对的边分别为a,b,c,sinA=$\frac{1}{4}$acosB,b=4$\sqrt{3}$.
如图,在△ABC中,角A,B,C所对的边分别为a,b,c,sinA=$\frac{1}{4}$acosB,b=4$\sqrt{3}$.