题目内容
6．设$\overrightarrow{a}$，$\overrightarrow{b}$是两个非零向量，若命题p：$\overrightarrow{a}$•$\overrightarrow{b}$＞0，命题q：$\overrightarrow{a}$，$\overrightarrow{b}$夹角是锐角，则命题p是命题q成立的（ ）| A． | 充分不必要条件 | B． | 必要不充分条件 | ||
| C． | 充要条件 | D． | 既不充分也不必要条件 |
分析 利用数量积运算性质、三角函数求值即可判断出结论．
解答 解：设$\overrightarrow{a}$，$\overrightarrow{b}$夹角是θ，
命题p：$\overrightarrow{a}$•$\overrightarrow{b}$＞0，则cosθ＞0，∴θ是锐角或0，
则命题p是命题q成立的必要不充分条件．
故选：B．
点评 本题考查了向量数量积运算性质、向量夹角、简易逻辑的判定方法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
已知点列Pn（xn，$\frac{2}{{x}_{n}}$）与An（an，0）满足xn+1＞xn，$\overrightarrow{{{P}_{n}P}_{n+1}}$⊥$\overrightarrow{{{A}_{n}P}_{n+1}}$，且|$\overrightarrow{{{P}_{n}P}_{n+1}}$|=|$\overrightarrow{{{A}_{n}P}_{n+1}}$|，其中n∈N*，x1=1．
17．执行如图的程序框图，若输入?=0.01，则输出的N=（ ）
| A． | 102 | B． | 101 | C． | 100 | D． | 99 |
11．齐王与田忌赛马，田忌的上等马优于齐王的中等马，劣于齐王的上等马，田忌的中等马优于齐王的下等马，劣于齐王的中等马，田忌的下等马劣于齐王的下等马，现从双方的马匹中随机选一匹马进行一场比赛，则田忌获胜的概率为（ ）
| A． | $\frac{1}{3}$ | B． | $\frac{1}{4}$ | C． | $\frac{1}{5}$ | D． | $\frac{1}{6}$ |
18．已知命题￢p：存在x∈（1，2）使得ex-a＞0，若p是真命题，则实数a的取值范围为（ ）
| A． | （-∞，e） | B． | （-∞，e] | C． | （e2，+∞） | D． | [e2，+∞） |
16．
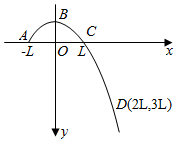从A点斜向上抛出一个小球，曲线ABCD是小球运动的一段轨迹，建立如图所示的正交坐标系xOy，x轴沿水平方向，轨迹上三个点的坐标分别为A（-L，0），C（L，0），D（2L，3L），小球受到的空气阻力忽略不计，轨迹与y轴的交点B的坐标为（ ）
从A点斜向上抛出一个小球，曲线ABCD是小球运动的一段轨迹，建立如图所示的正交坐标系xOy，x轴沿水平方向，轨迹上三个点的坐标分别为A（-L，0），C（L，0），D（2L，3L），小球受到的空气阻力忽略不计，轨迹与y轴的交点B的坐标为（ ）| A． | （0，-$\frac{L}{2}$） | B． | （0，-L） | C． | （0，-$\frac{3L}{2}$） | D． | （0，-2L） |