题目内容
已知函数f(x)=sin(ωx+φ)(ω>0,0≤φ≤π)是R上的偶函数,其图象关于点M(
,0)对称,且在区间[0,
]上是单调函数,
(1)求φ和ω的值;
(2)已知对任意x∈R函数g(x)满足g(π+x)=g(π-x),且当x∈(0,π)时,g(x)=f(x),试求:g(
).
| 3π |
| 4 |
| π |
| 2 |
(1)求φ和ω的值;
(2)已知对任意x∈R函数g(x)满足g(π+x)=g(π-x),且当x∈(0,π)时,g(x)=f(x),试求:g(
| 3π |
| 2 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的图象
专题:计算题,压轴题,数形结合,三角函数的图像与性质
分析:(1)由f(x)是偶函数可得ϕ的值,图象关于点M(
,0)对称可得函数关系f(
-x)=-f(
+x),可得ω的可能取值,结合单调函数可确定ω的值.
(2)由(1)得f(x)=sin(ωx+
)(ω>0,0≤φ≤π),又由题意可得函数图象关于x=π对称,即有ω×π+
=2kπ±
,k∈Z,结合(1)可得ω=2,从而求出解析式:g(x)=f(x)=sin(2x+
),即可求g(
)的值.
| 3π |
| 4 |
| 3π |
| 4 |
| 3π |
| 4 |
(2)由(1)得f(x)=sin(ωx+
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
解答:
解:(1)解:由f(x)是偶函数,得f(-x)=f(x),
即sin(-ωx+φ)=sin(ωx+φ),
所以-cosφsinωx=cosφsinωx,
对任意x都成立,且w>0,
所以得cosφ=0.
依题设0≤φ≤π,所以解得φ=
,
由f(x)的图象关于点M对称,
得f(
-x)=-f(
+x),
取x=0,得f(
)=sin(
+
)=cos
,
∴f(
)=sin(
+
)=cos
,
∴cos
=0,
又w>0,得
=
+kπ,k=0,1,2,3,…
∴ω=
(2k+1),k=0,1,2,…
当k=0时,ω=
,f(x)=sin(
x+
)在[0,
]上是减函数,满足题意;
当k=1时,ω=2,f(x)=sin(2x+
)=cos2x,在[0,
]上是减函数,满足题意;
当k=2时,ω=
,f(x)=sin(
x+
)在[0,
]上不是单调函数;
所以,综合得ω=
或2.
(2)∵由(1)得f(x)=sin(ωx+
)(ω>0,0≤φ≤π),
又∵对任意x∈R函数g(x)满足g(π+x)=g(π-x),且当x∈(0,π)时,g(x)=f(x),
∴由题意可得函数图象关于x=π对称,即有ω×π+
=2kπ±
,k∈Z,
∴从而解得:ω=2k或2k-1,k∈Z即ω是整数,
∴由(1)可得ω=2,g(x)=f(x)=sin(2x+
),
∴g(
)=sin(2×
+
)=-1.
即sin(-ωx+φ)=sin(ωx+φ),
所以-cosφsinωx=cosφsinωx,
对任意x都成立,且w>0,
所以得cosφ=0.
依题设0≤φ≤π,所以解得φ=
| π |
| 2 |
由f(x)的图象关于点M对称,
得f(
| 3π |
| 4 |
| 3π |
| 4 |
取x=0,得f(
| 3π |
| 4 |
| 3ωπ |
| 4 |
| π |
| 2 |
| 3ωπ |
| 4 |
∴f(
| 3π |
| 4 |
| 3ωπ |
| 4 |
| π |
| 2 |
| 3ωπ |
| 4 |
∴cos
| 3ωπ |
| 4 |
又w>0,得
| 3ωπ |
| 4 |
| π |
| 2 |
∴ω=
| 2 |
| 3 |
当k=0时,ω=
| 2 |
| 3 |
| 2 |
| 3 |
| π |
| 2 |
| π |
| 2 |
当k=1时,ω=2,f(x)=sin(2x+
| π |
| 2 |
| π |
| 2 |
当k=2时,ω=
| 10 |
| 3 |
| 10 |
| 3 |
| π |
| 2 |
| π |
| 2 |
所以,综合得ω=
| 2 |
| 3 |
(2)∵由(1)得f(x)=sin(ωx+
| π |
| 2 |
又∵对任意x∈R函数g(x)满足g(π+x)=g(π-x),且当x∈(0,π)时,g(x)=f(x),
∴由题意可得函数图象关于x=π对称,即有ω×π+
| π |
| 2 |
| π |
| 2 |
∴从而解得:ω=2k或2k-1,k∈Z即ω是整数,
∴由(1)可得ω=2,g(x)=f(x)=sin(2x+
| π |
| 2 |
∴g(
| 3π |
| 2 |
| 3π |
| 2 |
| π |
| 2 |
点评:本题主要考查三角函数的图象、单调性、对称性、奇偶性等基本知识,以及分析问题和推理计算能力,考察了数形结合的能力,综合性强,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
数列{an}的通项公式为an=(-1)n+1•
,则a7=( )
| n+1 |
| n |
| A、8 | ||
B、-
| ||
C、
| ||
| D、7 |
用“二分法”求方程x3-2x-1=0的一个近似解时,现在已经将一根锁定在在区间(1,2)内,则下一步可断定该根所在的区间为( )
| A、(1,1.4) |
| B、(1.4,2) |
| C、(1,1.5) |
| D、(1.5,2) |
已知函数f(x)=2sinx(α为常数),则f′(α)=( )
| A、2cosα |
| B、0 |
| C、cos2α |
| D、2sinα |
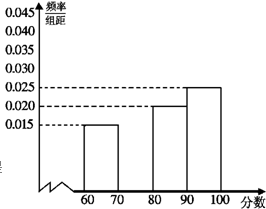 某集团公司对所属的200家企业进行年终考评,并依据考评得分(最低60分,最高100分,可以是小数)将其分别评定为A、B、C、D四个等级,标准如下表:
某集团公司对所属的200家企业进行年终考评,并依据考评得分(最低60分,最高100分,可以是小数)将其分别评定为A、B、C、D四个等级,标准如下表: