题目内容
过双曲线
-
=1(a>0,b>0)的左焦点F作圆x2+y2=a2的切线,切点为T,延长FT交双曲线右支于点P,若线段PF的中点为M,O为坐标原点,M在线段TP上,则|OM|-|MT|的值为( )
| x2 |
| a2 |
| y2 |
| b2 |
| A、b-a | B、a-b |
| C、b | D、不确定 |
考点:双曲线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:如图所示,设F′是双曲线的右焦点,连接PF′.利用三角形的中位线定理和双曲线的定义可得:|OM|=
|PF′|=
(|PF|-2a)=
|PF|-a=|MF|-a,于是|OM|-|MT|=|MF|-|MT|-a=|FT|-a,连接OT,则OT⊥FT,在Rt△FOT中,|OF|=c,|OT|=a,可得|FT|=
=b.即可得出关系式.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| |OF|2-|OT|2 |
解答:
解:如图所示,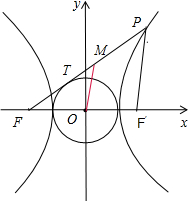
设F′是双曲线的右焦点,连接PF′.
∵点M,O分别为线段PF,FF′的中点,
由三角形中位线定理得到:|OM|=
|PF′|=
(|PF|-2a)=
|PF|-a=|MF|-a,
∴|OM|-|MT|=|MF|-|MT|-a=|FT|-a,连接OT,因为PT是圆的切线,则OT⊥FT,
在Rt△FOT中,|OF|=c,|OT|=a,∴|FT|=
=b.
∴|OM|-|MT|=b-a.
故选A.

设F′是双曲线的右焦点,连接PF′.
∵点M,O分别为线段PF,FF′的中点,
由三角形中位线定理得到:|OM|=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴|OM|-|MT|=|MF|-|MT|-a=|FT|-a,连接OT,因为PT是圆的切线,则OT⊥FT,
在Rt△FOT中,|OF|=c,|OT|=a,∴|FT|=
| |OF|2-|OT|2 |
∴|OM|-|MT|=b-a.
故选A.
点评:本题考查了双曲线的定义和性质的运用,结合三角形的中位线定理、直线与圆相切的性质等知识,考查学生的计算能力和分析能力,是难题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
关于x的二次方程(
•
)x2+4(
•
)x+(
•
)=0没有实数根,则向量
与
的夹角的范围为( )
| a |
| a |
| a |
| b |
| b |
| b |
| a |
| b |
A、[0,
| ||||
B、[0,
| ||||
C、(
| ||||
D、(
|
双曲线
-
=1的渐近线方程是( )
| x2 |
| 4 |
| y2 |
| 9 |
A、y=±
| ||
B、y=±
| ||
C、y=±
| ||
D、y=±
|
椭圆的长轴长为10,一个焦点坐标为(4,0),则它的标准方程为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
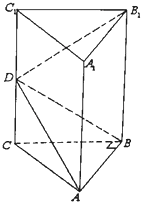 如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,CC1=2AB=2BC=2,D是CC1中点
如图,在直三棱柱ABC-A1B1C1中,∠ABC=90°,CC1=2AB=2BC=2,D是CC1中点