Question

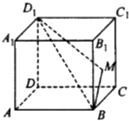如图，在正方体ABCD-A₁B₁C₁D₁中，当动点M在侧面BCC₁B₁内运动时，总有∠MD₁D=∠BD₁D，则动点M在平面BCC₁B₁内的转迹是（　　）

• A、圆的一部分
• B、椭圆的一部分
• C、双曲线的一部分
• D、抛物线的一部分

Answer 1

考点：轨迹方程

专题：综合题,圆锥曲线的定义、性质与方程,空间位置关系与距离

分析：以D为坐标原点，DA为x轴，DC为y轴，DD₁为z轴，建立空间直角坐标系，利用向量法能求出点M的轨迹是双曲线的一部分．

解答： 解：以D为坐标原点，DA为x轴，DC为y轴，DD₁为z轴，建立空间直角坐标系，
设AB=1，M（x，1，z），D（0，0，0），D₁（0，0，1）B（1，1，0），
∴

D1B

=（1，1，-1），

D1D

=（0，0，-1），

D1M

=（x，1，z-1），
∵∠MD₁D=∠BD₁D＜

π

2

，
∴cos∠MD₁D=cos∠BD₁D，
∴

(z-1)•(-1)

x2+1+(z-1)2

=

1

3

，
整理，得x²-2z²+4z=1，（0＜x＜1，0＜z＜1），
∴点M的轨迹是双曲线的一部分．
故选：C．

点评：本题考查点的轨迹的求法，是中档题，解题时要认真审题，注意向量法的合理运用．