题目内容
定义:eiθ=cosθ+isinθ(i为虚数单位),若ei
+1-
i=eiα,则α角可能是( )
| 2π |
| 3 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:复数代数形式的混合运算
专题:数系的扩充和复数
分析:把ei
用cos
+isin
替换,代入对应的三角函数值,然后利用复数代数形式的加减运算整理,进一步结合eiα=cosα+isinα求得α的值.
| 2π |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
解答:
解:由eiθ=cosθ+isinθ,得
eiα=cosα+isinα,
∴ei
+1-
i=cos
+isin
+1-
i
=-
+
i+1-
i=
-
i=cos
+isin
=ei
=eiα.
∴α=
.
故选:C.
eiα=cosα+isinα,
∴ei
| 2π |
| 3 |
| 3 |
| 2π |
| 3 |
| 2π |
| 3 |
| 3 |
=-
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 5π |
| 3 |
| 5π |
| 3 |
| 5π |
| 3 |
∴α=
| 5π |
| 3 |
故选:C.
点评:本题考查复数代数形式的混合运算,考查了三角函数的值,是中档题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
设p、q是简单命题,则“p∧q为真”是“p∨q为真”的( )
| A、充分但不必要条件 |
| B、必要但不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
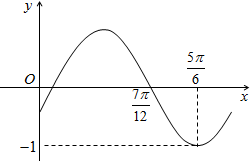
已知函数y=sin(ωx+φ)(ω>0,-
<φ<
)的部分图象如图所示,则( )
| π |
| 2 |
| π |
| 2 |

A、ω=2,φ=-
| ||
B、ω=2,φ=
| ||
C、ω=1,φ=-
| ||
D、ω=1,φ=
|
用一个平面去截一个正方体,所得截面不可能是
(1)钝角三角形;
(2)直角三角形;
(3)菱形;
(4)正五边形;
(5)正六边形.
下述选项正确的是( )
(1)钝角三角形;
(2)直角三角形;
(3)菱形;
(4)正五边形;
(5)正六边形.
下述选项正确的是( )
| A、(1)(2)(5) |
| B、(1)(2)(4) |
| C、(2)(3)(4) |
| D、(3)(4)(5) |
若x,y满足约束条件
,则z=2x+y的最小值是( )
|
| A、-1 | B、0 | C、2 | D、8 |
若S={1,2,3,4,5},M={1,3,4},N={2,4,5},则(∁SM)∩(∁SN)等于( )
| A、{1,3} | B、∅ |
| C、{4} | D、{2,5} |
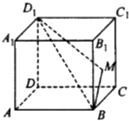 如图,在正方体ABCD-A1B1C1D1中,当动点M在侧面BCC1B1内运动时,总有∠MD1D=∠BD1D,则动点M在平面BCC1B1内的转迹是( )
如图,在正方体ABCD-A1B1C1D1中,当动点M在侧面BCC1B1内运动时,总有∠MD1D=∠BD1D,则动点M在平面BCC1B1内的转迹是( )| A、圆的一部分 |
| B、椭圆的一部分 |
| C、双曲线的一部分 |
| D、抛物线的一部分 |
设集合A={x|(x+1)(x-5)>0},B={x|a<x<a+8},若A∪B=R,则实数a的取值范围是( )
| A、-3<a<-1 |
| B、-3≤a≤-1 |
| C、a≤-3或a≥-1 |
| D、a<-3或a>-1 |