题目内容
在△ABC中,|
|=2,|
|=1,
•
=-1,则△ABC的外接圆半径是( )
| BA |
| AC |
| BA |
| AC |
| A、1 | ||||
| B、2 | ||||
C、
| ||||
D、
|
考点:正弦定理
专题:解三角形
分析:利用平面向量的数量积运算列出关系式,将已知等式代入计算求出cosA的值,确定出A的度数,再利用正弦定理即可求出外接圆半径.
解答:
解:∵在△ABC中,|
|=2,|
|=1,
•
=-1,
∴2×1×cos(π-A)=-1,即cosA=
,
∴A=60°,
由余弦定理得:|
|2=4+1-2=3,即|
|=
,
则由正弦定理得:2R=
=2,即R=1,
故选:A.
| BA |
| AC |
| BA |
| AC |
∴2×1×cos(π-A)=-1,即cosA=
| 1 |
| 2 |
∴A=60°,
由余弦定理得:|
| BC |
| BC |
| 3 |
则由正弦定理得:2R=
| ||
| sin60° |
故选:A.
点评:此题考查了正弦定理,平面向量的数量积运算,熟练掌握正弦定理是解本题的关键.

练习册系列答案
相关题目
若a∈R,则复数z=
对应的点不可能在复平面的( )
| a+i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
设p、q是简单命题,则“p∧q为真”是“p∨q为真”的( )
| A、充分但不必要条件 |
| B、必要但不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
在数列{an}中,a1=1,a2=2,且an+2-an=1+(-1)n(n∈N*),则S100=( )
| A、2100 | B、2600 |
| C、2800 | D、3100 |
如图程序运行后输出的结果为( )


| A、10 | B、9 | C、6 | D、5 |
函数y=x2(x≤0)的反函数是( )
A、y=
| ||
B、y=
| ||
C、y=-
| ||
D、y=-
|
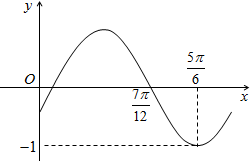
已知函数y=sin(ωx+φ)(ω>0,-
<φ<
)的部分图象如图所示,则( )
| π |
| 2 |
| π |
| 2 |

A、ω=2,φ=-
| ||
B、ω=2,φ=
| ||
C、ω=1,φ=-
| ||
D、ω=1,φ=
|
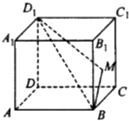 如图,在正方体ABCD-A1B1C1D1中,当动点M在侧面BCC1B1内运动时,总有∠MD1D=∠BD1D,则动点M在平面BCC1B1内的转迹是( )
如图,在正方体ABCD-A1B1C1D1中,当动点M在侧面BCC1B1内运动时,总有∠MD1D=∠BD1D,则动点M在平面BCC1B1内的转迹是( )| A、圆的一部分 |
| B、椭圆的一部分 |
| C、双曲线的一部分 |
| D、抛物线的一部分 |