题目内容
M是椭圆
+
=1上一点，F1，F2是其左右焦点，则满足∠F1MF2=
的点M的个数是（ ）
| x2 |
| 16 |
| y2 |
| 9 |
| π |
| 2 |
| A、0 | B、1 | C、2 | D、4 |
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：当M是椭圆的短轴的一个端点时，∠F1MF2是椭圆上的点到F1，F2张开的角中的最大角，即可判断出．
解答：
解：由椭圆
+
=1可得：a=4，b=3，c=
，
当M是椭圆的短轴的一个端点（0，3）时，tan∠OMF2=
=
＜1，可得∠F1MF2＜
，
而∠F1MF2是椭圆上的点到F1，F2张开的角中的最大角，
因此满足∠F1MF2=
的点M的个数是0．
故选：A．
| x2 |
| 16 |
| y2 |
| 9 |
| 7 |
当M是椭圆的短轴的一个端点（0，3）时，tan∠OMF2=
| c |
| b |
| ||
| 3 |
| π |
| 2 |
而∠F1MF2是椭圆上的点到F1，F2张开的角中的最大角，
因此满足∠F1MF2=
| π |
| 2 |
故选：A．
点评：本题考查了椭圆上的点到焦点F1，F2张开的角中的最大角的性质，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
如图程序运行后输出的结果为（ ）
| A、10 | B、9 | C、6 | D、5 |
用一个平面去截一个正方体，所得截面不可能是
（1）钝角三角形；
（2）直角三角形；
（3）菱形；
（4）正五边形；
（5）正六边形．
下述选项正确的是（ ）
（1）钝角三角形；
（2）直角三角形；
（3）菱形；
（4）正五边形；
（5）正六边形．
下述选项正确的是（ ）
| A、（1）（2）（5） |
| B、（1）（2）（4） |
| C、（2）（3）（4） |
| D、（3）（4）（5） |
若S={1，2，3，4，5}，M={1，3，4}，N={2，4，5}，则（∁SM）∩（∁SN）等于（ ）
| A、{1，3} | B、∅ |
| C、{4} | D、{2，5} |
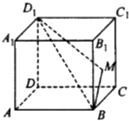如图，在正方体ABCD-A1B1C1D1中，当动点M在侧面BCC1B1内运动时，总有∠MD1D=∠BD1D，则动点M在平面BCC1B1内的转迹是（ ）| A、圆的一部分 |
| B、椭圆的一部分 |
| C、双曲线的一部分 |
| D、抛物线的一部分 |
已知复数z1=3+4i，z2=t+i，且z1•
是实数，则t=（ ）
. |
| z2 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
设集合A={x|（x+1）（x-5）＞0}，B={x|a＜x＜a+8}，若A∪B=R，则实数a的取值范围是（ ）
| A、-3＜a＜-1 |
| B、-3≤a≤-1 |
| C、a≤-3或a≥-1 |
| D、a＜-3或a＞-1 |