题目内容
已知c>0,设p:函数f(x)=cx在R上单调递减,q:函数g(x)=
的定义域是R,如果“p且q”是假命题,“p或q”是真命题,那么c的取值范围是( )
| 1 |
| 2cx2+2x+1 |
A、(
| ||
B、(
| ||
C、(0,
| ||
D、(0,
|
考点:复合命题的真假
专题:简易逻辑
分析:根据已知条件可知,命题p和q的真假情况分成有一个为真,一个为假两种情况.所以先分别求出p,q为真时的c的取值范围,从而求出c在每种情况下的取值范围,把这两种情况合并在一块,便能得到c的取值范围.
解答:
解:由已知条件可知:p和q中有一个真命题,一个假命题.
(1)若p真,q假,则:
由p得:0<c<1.
由函数g(x)=
的定义域是R得:
,解得:c>
;
∴q为假时,c≤
;
∴c的取值范围是:(0,
].
(2)若p假q真,则:c≥1,且c>
;
∴c的取值范围是[1,+∞).
综上可得a的取值范围是:(0,
]∪[1,+∞).
故选C.
(1)若p真,q假,则:
由p得:0<c<1.
由函数g(x)=
| 1 |
| 2cx2+2x+1 |
|
| 1 |
| 2 |
∴q为假时,c≤
| 1 |
| 2 |
∴c的取值范围是:(0,
| 1 |
| 2 |
(2)若p假q真,则:c≥1,且c>
| 1 |
| 2 |
∴c的取值范围是[1,+∞).
综上可得a的取值范围是:(0,
| 1 |
| 2 |
故选C.
点评:本题考查考查真命题,假命题的概念,指数函数的单调性,一元二次方程解情况的,复合命题p且q真假情况.

练习册系列答案
相关题目
若a∈R,则复数z=
对应的点不可能在复平面的( )
| a+i |
| 1+i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
函数y=x2(x≤0)的反函数是( )
A、y=
| ||
B、y=
| ||
C、y=-
| ||
D、y=-
|
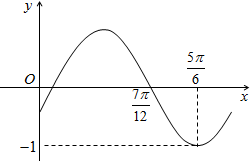
已知函数y=sin(ωx+φ)(ω>0,-
<φ<
)的部分图象如图所示,则( )
| π |
| 2 |
| π |
| 2 |

A、ω=2,φ=-
| ||
B、ω=2,φ=
| ||
C、ω=1,φ=-
| ||
D、ω=1,φ=
|
已知集合A={x∈Z|x2-2x≤0},集合B={x|x=2a,a∈A},则A∩B为( )
| A、{0} | B、{2} |
| C、{0,2} | D、{1,4} |
用一个平面去截一个正方体,所得截面不可能是
(1)钝角三角形;
(2)直角三角形;
(3)菱形;
(4)正五边形;
(5)正六边形.
下述选项正确的是( )
(1)钝角三角形;
(2)直角三角形;
(3)菱形;
(4)正五边形;
(5)正六边形.
下述选项正确的是( )
| A、(1)(2)(5) |
| B、(1)(2)(4) |
| C、(2)(3)(4) |
| D、(3)(4)(5) |
若x,y满足约束条件
,则z=2x+y的最小值是( )
|
| A、-1 | B、0 | C、2 | D、8 |
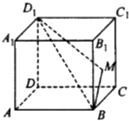 如图,在正方体ABCD-A1B1C1D1中,当动点M在侧面BCC1B1内运动时,总有∠MD1D=∠BD1D,则动点M在平面BCC1B1内的转迹是( )
如图,在正方体ABCD-A1B1C1D1中,当动点M在侧面BCC1B1内运动时,总有∠MD1D=∠BD1D,则动点M在平面BCC1B1内的转迹是( )| A、圆的一部分 |
| B、椭圆的一部分 |
| C、双曲线的一部分 |
| D、抛物线的一部分 |