题目内容
设函数f（x）=
，若f（x）＞f（0），则x的取值范围是（ ）
|
| A、（0，2）∪（3，+∞） |
| B、（3，+∞） |
| C、（0，1）∪（2，+∞） |
| D、（0，2） |
考点：函数单调性的判断与证明,函数单调性的性质
专题：函数的性质及应用
分析：f（x）是分段函数，先求出f（0），然后在每段函数里求x的取值范围，从而求出x的取值范围．
解答：
解：f（0）=1
∴x＜2时，由2x＞1得：0＜x＜2；
x≥2时，由
＞1得：x＞3．
∴x的取值范围是（0，2）∪（3，+∞）．
故选：A．
∴x＜2时，由2x＞1得：0＜x＜2；
x≥2时，由
| 2x |
| x+3 |
∴x的取值范围是（0，2）∪（3，+∞）．
故选：A．
点评：考查分段函数的求值，对于解不等式f（x）＞f（0），要在每段函数里求解．
练习册系列答案
课堂练加测系列答案
轻松课堂单元测试AB卷系列答案
相关题目
已知函数y=sin（ωx+φ）（ω＞0，-
＜φ＜
）的部分图象如图所示，则（ ）
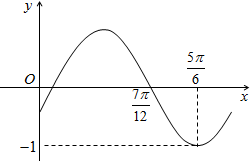
| π |
| 2 |
| π |
| 2 |
A、ω=2，φ=-
| ||
B、ω=2，φ=
| ||
C、ω=1，φ=-
| ||
D、ω=1，φ=
|
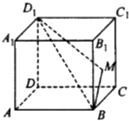如图，在正方体ABCD-A1B1C1D1中，当动点M在侧面BCC1B1内运动时，总有∠MD1D=∠BD1D，则动点M在平面BCC1B1内的转迹是（ ）| A、圆的一部分 |
| B、椭圆的一部分 |
| C、双曲线的一部分 |
| D、抛物线的一部分 |
设集合A={x|（x+1）（x-5）＞0}，B={x|a＜x＜a+8}，若A∪B=R，则实数a的取值范围是（ ）
| A、-3＜a＜-1 |
| B、-3≤a≤-1 |
| C、a≤-3或a≥-1 |
| D、a＜-3或a＞-1 |
| 3 | a2 |
|
A、a
| ||
B、a
| ||
C、a
| ||
D、a
|
已知正方体ABCD-A1B1C1D1，求证：