题目内容
圆台上的上、下底面半径分别为10和20，它的侧面展开图扇环的圆心角为π，则圆台的表面积为 ．
考点：旋转体（圆柱、圆锥、圆台）
专题：计算题,空间位置关系与距离
分析：解答本题可把空间问题转化为平面问题，即先在展开图内求母线的长，再进一步代入侧面积公式求出侧面积，进而求出表面积．
解答：
解：设圆台的上底面周长为c，因为扇环的圆心角是180°，?故c=π•SA=2π×10，?所以SA=20．?
同理可得SB=40，?
所以AB=SB-SA=20．?
所以S表面积=S侧+S上+S下
=π （r1+r2）•AB+πr12+πr22?
=π （10+20）×20+π×102+π×202?
=1100π．?
故圆台的表面积为1100π．
故答案为：1100π．
解：设圆台的上底面周长为c，因为扇环的圆心角是180°，?故c=π•SA=2π×10，?所以SA=20．?同理可得SB=40，?
所以AB=SB-SA=20．?
所以S表面积=S侧+S上+S下
=π （r1+r2）•AB+πr12+πr22?
=π （10+20）×20+π×102+π×202?
=1100π．?
故圆台的表面积为1100π．
故答案为：1100π．
点评：本题考查了圆台的侧面积、表面积、体积公式，熟练掌握圆台的侧面展开图扇环的圆心角公式是解答本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
如图，在正三棱柱ABC-A1B1C1中，AA1=AB，F、F1分别是AC、A1C1的中点．已知点P的极坐标是（2，π），则过点P且垂直极轴的直线方程是（ ）
| A、p=2 | ||
| B、p=2cosθ | ||
C、p=-
| ||
D、p=
|
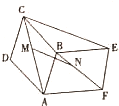如图所示，ABCD-ABEF都是平行四边形，且不共面，M、N分别是AC、BF的中点，判断