题目内容
已知x,y∈R+,4x2+9y2=36,则x+2y的最大值等于 .
考点:椭圆的参数方程,三角函数的最值
专题:坐标系和参数方程
分析:化椭圆的方程为参数方程
,其中θ∈(0,
),可得x+2y=3cosθ+4sinθ=5sin(θ+φ),由三角函数最值可得.
|
| π |
| 2 |
解答:
解:∵x,y∈R+,4x2+9y2=36,
∴
+
=1,为椭圆的方程
化为参数方程可得
,其中θ∈(0,
),
∴x+2y=3cosθ+4sinθ=5sin(θ+φ),其中tanφ=
由三角函数可知当5sin(θ+φ)=1时,x+2y取最大值5
故答案为:5
∴
| x2 |
| 9 |
| y2 |
| 4 |
化为参数方程可得
|
| π |
| 2 |
∴x+2y=3cosθ+4sinθ=5sin(θ+φ),其中tanφ=
| 3 |
| 4 |
由三角函数可知当5sin(θ+φ)=1时,x+2y取最大值5
故答案为:5
点评:本题考查椭圆的参数方程,涉及三角函数的运算,属基础题.

练习册系列答案
相关题目
定义在集合{1,2,3,4}上的函数f(x),g(x)分别由下表给出:
则与f[g(1)]相同的是( )
| x | 1 | 2 | 3 | 4 | x | 1 | 2 | 3 | 4 | |
| f(x) | 3 | 4 | 2 | 1 | g(x) | 4 | 3 | 1 | 2 |
| A、g(f(3)) |
| B、g(f(1)) |
| C、g(f(4)) |
| D、g(f(2)) |
已知定义在R的函数f(x),其导函数f′(x)的部分图象如图所示,则下列判断一定正确的是( )
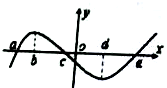

| A、f(a)=f(c)=f(e) |
| B、f(b)>f(c)>f(d) |
| C、f(c)>f(b)>f(a) |
| D、f(c)>f(d)>f(a) |
