题目内容
3.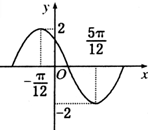 已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)在一个周期内的图象如图所示.
已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)在一个周期内的图象如图所示.(1)求函数f(x)的解析式与单调递减区间;
(2)函数f(x)的图象上所有点的横坐标扩大到原来的2倍,再向右平移$\frac{π}{2}$个单位长度,得到g(x)的图象,求函数y=g(x)在x∈[0,π]上的最大值及最小值.
分析 (1)利用图象,求出相应参数,即可求函数f(x)的解析式与单调递减区间;
(2)利用函数y=Asin(ωx+φ)的图象变换可得g(x)=2sin(x+$\frac{π}{6}$),由x∈[0,π]得x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],利用正弦函数的图象即可解得函数y=g(x)在x∈[0,π]上的最大值及最小值.
解答 解:(1)由图知,函数的最大值,最小值为2,-2,知A=2;
从最高点到最低点,自变量增加$\frac{π}{2}$,则$\frac{T}{2}=\frac{π}{2}$,T=π,$ω=\frac{2π}{π}=2$,
由五点法作图知$2(-\frac{π}{12})+ϕ=\frac{π}{2}$,则$ϕ=\frac{2}{3}π$,
所以$f(x)=2sin(2x+\frac{2}{3}π)$函数的周期为π,且由图知函数的一个单调递减区间为$(-\frac{π}{12},\frac{5}{12}π)$
因此f(x)的单调递减区间为$(-\frac{π}{12}+kπ,\frac{5}{12}π+kπ),k∈Z$;
(2)由题意,g(x)=2sin(x+$\frac{π}{6}$),
∵x∈[0,π],
∴x+$\frac{π}{6}$∈[$\frac{π}{6}$,$\frac{7π}{6}$],
∴函数y=g(x)在x∈[0,π]上的最大值为2,最小值为-1.
点评 本题主要考查了正弦函数的图象和性质,函数y=Asin(ωx+φ)的图象变换规律,属于中档题.

练习册系列答案
相关题目
11.某三角形两边之差为2,它们的夹角正弦值为$\frac{4}{5}$,面积为14,那么这两边长分别是( )
| A. | 3和5 | B. | 4和6 | C. | 6和8 | D. | 5和7 |
8.已知定义在R上的函数f(x)满足f(x)+f(-x)=2x2,且x∈[0,+∞)时f′(x)>2x恒成立,则不等式f(8-x)+16x<64+f(x)的解集为( )
| A. | (4,+∞) | B. | (-∞,4) | C. | (8,+∞) | D. | (-∞,8) |
15.如果函数y=3cos(2x+φ)的图象关于点$({\frac{4π}{3},0})$,则|φ|的最小值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |