题目内容
8.已知定义在R上的函数f(x)满足f(x)+f(-x)=2x2,且x∈[0,+∞)时f′(x)>2x恒成立,则不等式f(8-x)+16x<64+f(x)的解集为( )| A. | (4,+∞) | B. | (-∞,4) | C. | (8,+∞) | D. | (-∞,8) |
分析 根据题意,令g(x)=f(x)-x2,分析可得g(x)为奇函数且在R为增函数,f(8-x)+16x<64+f(x)转化可得f(8-x)-(64-16x+x2)<f(x)-x2,即g(8-x)<g(x),结合g(x)的单调性可得8-x<x,解可得x的取值范围.
解答 解:根据题意,令g(x)=f(x)-x2,
若f(x)+f(-x)=2x2,变形有f(x)-x2+f(-x)-(-x)2=0,
即g(x)+g(-x)=0,故g(x)为奇函数,
g(x)=f(x)-x2,g′(x)=f′(x)-2x,
又由x∈[0,+∞)时f′(x)>2x恒成立,则x>0时,g′(x)=f′(x)-2x>0恒成立,
即g(x)在[0,+∞)为增函数,
又由g(x)为奇函数,则g(x)在(-∞,0)也为增函数,
综合可得:g(x)在R为增函数;
不等式f(8-x)+16x<64+f(x),
则有f(8-x)-(64-16x+x2)<f(x)-x2,
即g(8-x)<g(x),
则有8-x<x,
解可得x>4,
即不等式f(8-x)+16x<64+f(x)的解集为(4,+∞);
故选:A.
点评 本题考查函数单调性的应用,涉及利用导数判断函数的单调性,关键是构造g(x),并分析函数g(x)的奇偶性、单调性.

练习册系列答案
相关题目
13.设x,y,z均为正实数,a=x+$\frac{1}{y}$,b=y+$\frac{1}{z}$,c=z+$\frac{1}{x}$,则a,b,c三个数( )
| A. | 至少有一个不小于2 | B. | 都小于2 | ||
| C. | 至少有一个不大于2 | D. | 都大于2 |
20.关于圆周率π,数学发展史上出现过许多很有创意的求法,如著名的普丰实验和查理斯实验,受其启发,我们也可以通过设计下面的实验来估计π的值,先请120名同学每人随机写下一个都小于1的正实数对(x,y),再统计两数能与1构成钝角三角形三边的数对(x,y)的个数m;最后在根据统计数m估计π的值,假设统计结果是m=34,那么可以估计π的值为( )
| A. | $\frac{22}{7}$ | B. | $\frac{47}{15}$ | C. | $\frac{51}{16}$ | D. | $\frac{53}{17}$ |
17.圆(x-2)2+y2=4与圆x2+(y-2)2=4在公共弦所对的圆心角是( )
| A. | $\frac{π}{3}$ | B. | $\frac{π}{4}$ | C. | $\frac{2π}{3}$ | D. | $\frac{π}{2}$ |
18.已知集合 A={x|-2<x<3},B={x|x≥m}.若 A∩B=∅,则实数m的取值范围是( )
| A. | (-∞,3] | B. | (-2,3] | C. | (-∞,-2) | D. | [3,+∞) |
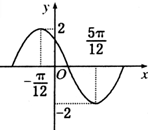 已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)在一个周期内的图象如图所示.
已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)在一个周期内的图象如图所示.