题目内容
13.在△ABC中,∠A,∠B,∠C所对的边分别是a,b,c.当钝角△ABC的三边a,b,c是三个连续整数时,则△ABC外接圆的半径为$\frac{{8\sqrt{15}}}{15}$.分析 由题意设出钝角三角形的三边长分别为x,x+1,x+2,可得出x+2所对的角为钝角,设为α,利用余弦定理表示出cosα,将设出的三边代入,根据cosα小于0,得出x的范围,在范围中找出整数x的值,确定出三角形的三边长,进而确定出cosα的值,利用同角三角函数间的基本关系求出sinα的值,利用正弦定理即可求出三角形ABC外接圆的半径.
解答 解:由题意得:钝角△ABC的三边分别为x,x+1,x+2,且x+2所对的角为钝角α,
∴由余弦定理得:cosα=$\frac{{x}^{2}+(x+1)^{2}-(x+2)^{2}}{2x(x+1)}$=$\frac{x-3}{2x}$<0,即x<3,
∴x=1或x=2,
当x=1时,三角形三边分别为1,2,3,不能构成三角形,舍去;
当x=2时,三角形三边长分别为2,3,4,此时cosα=-$\frac{1}{4}$,
∴sinα=$\sqrt{1-co{s}^{2}α}$=$\frac{\sqrt{15}}{4}$,
设△ABC外接圆的半径为R,根据正弦定理得:$\frac{4}{\frac{\sqrt{15}}{4}}$=2R,
解得:R=$\frac{{8\sqrt{15}}}{15}$.
故答案为:$\frac{{8\sqrt{15}}}{15}$.
点评 此题考查了正弦、余弦定理,以及同角三角函数间的基本关系,熟练掌握正弦、余弦定理是解本题的关键,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.设(1+i)x=1+yi,x,y∈R,则|x+yi|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
8.已知tanθ=4,则$\frac{sinθ+cosθ}{17sinθ}+\frac{{si{n^2}θ}}{4}$的值为( )
| A. | $\frac{14}{68}$ | B. | $\frac{21}{68}$ | C. | $\frac{68}{14}$ | D. | $\frac{68}{21}$ |
5.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上是增函数.令a=f(sin50°),b=f[cos(-50°)],c=f(-tan50°),则( )
| A. | b<a<c | B. | c<b<a | C. | b<c<a | D. | a<b<c |
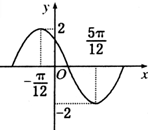 已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)在一个周期内的图象如图所示.
已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)在一个周期内的图象如图所示.