题目内容
18．已知sinα+cosα=$\frac{1}{5}$ 且 0＜α＜π求：（1）sinαcosα；
（2）tanα．
分析 （1）已知等式两边平方，利用完全平方公式及同角三角函数间的基本关系化简即可求出所求；
（2）求出sinα与cosα的值，原式利用同角三角函数间的基本关系化简后，将各自的值代入计算即可求出值．
解答 解：（1）∵sinα+cosα=$\frac{1}{5}$，
∴（sinα+cosα）2=1+2sinαcosα=$\frac{1}{25}$，
则sinαcosα=-$\frac{12}{25}$；
（2）∵sinα+cosα=$\frac{1}{5}$①，2sinαcosα=-$\frac{24}{25}$，
∴（sinα-cosα）2=1-2sinαcosα=$\frac{49}{25}$，
∵0＜α＜π，
∴sinα-cosα=$\frac{7}{5}$②，
联立①②，解得：sinα=$\frac{4}{5}$，cosα=-$\frac{3}{5}$，
则tanα=$\frac{sinα}{cosα}$=-$\frac{4}{3}$．
点评 此题考查了同角三角函数间的基本关系，熟练掌握同角三角函数的基本关系是解本题的关键．
练习册系列答案
相关题目
8．已知tanθ=4，则$\frac{sinθ+cosθ}{17sinθ}+\frac{{si{n^2}θ}}{4}$的值为（ ）
| A． | $\frac{14}{68}$ | B． | $\frac{21}{68}$ | C． | $\frac{68}{14}$ | D． | $\frac{68}{21}$ |
13．已知函数y=sin（2x+φ）+1的图象关于直线$x=-\frac{π}{8}$对称，则φ的可能取值是（ ）
| A． | $\frac{3π}{4}$ | B． | $-\frac{3π}{4}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{2}$ |
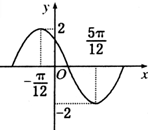已知函数f（x）=Asin（ωx+ϕ）（A＞0，ω＞0，|ϕ|＜π）在一个周期内的图象如图所示．
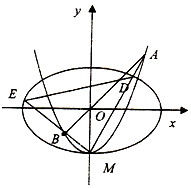如图，椭圆C1：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，x轴被曲线C2：y=x2-b截得的线段长等于C1的短轴长，C2与y轴的交点为M，过坐标原点O的直线l与C2相交于点A、B，直线MA，MB分别与C1相交于点D、E．