题目内容
11.某三角形两边之差为2,它们的夹角正弦值为$\frac{4}{5}$,面积为14,那么这两边长分别是( )| A. | 3和5 | B. | 4和6 | C. | 6和8 | D. | 5和7 |
分析 利用面积公式S△ABC=$\frac{1}{2}$acsinB,即可得出ac的值,与a-c=2联立即可得出a,c得值.
解答 解:如图所示, 假设已知a-c=2,sinB=$\frac{4}{5}$,
假设已知a-c=2,sinB=$\frac{4}{5}$,
S△ABC=$\frac{1}{2}acsinB$=14,∴ac=35.
结合a-c=2,∵a,c>0,解得a=7,c=5
故选:D.
点评 本题考查余弦定理的应用. 面积公式的应用,属于基础题.

练习册系列答案
相关题目
1.设(1+i)x=1+yi,x,y∈R,则|x+yi|=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
20.关于圆周率π,数学发展史上出现过许多很有创意的求法,如著名的普丰实验和查理斯实验,受其启发,我们也可以通过设计下面的实验来估计π的值,先请120名同学每人随机写下一个都小于1的正实数对(x,y),再统计两数能与1构成钝角三角形三边的数对(x,y)的个数m;最后在根据统计数m估计π的值,假设统计结果是m=34,那么可以估计π的值为( )
| A. | $\frac{22}{7}$ | B. | $\frac{47}{15}$ | C. | $\frac{51}{16}$ | D. | $\frac{53}{17}$ |
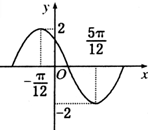 已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)在一个周期内的图象如图所示.
已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)在一个周期内的图象如图所示.