题目内容
13.祖暅是南北朝时代的伟大科学家,5世纪末提出体积计算原理,即祖暅原理:“幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等,现有以下四个几何体:图①是从圆柱中挖去一个圆锥所得的几何体;图②、图③、图④分别是圆锥、圆台和半球,则满足祖暅原理的两个几何体为( )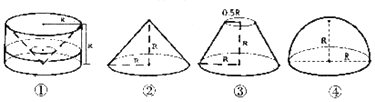
| A. | ①② | B. | ①③ | C. | ②④ | D. | ①④ |
分析 利用祖暅原理分析题设中的四个图形,能够得到在①和④中的两个几何体满足祖暅原理.
解答 解:在①和④中,
夹在两个平行平面之间的这两个几何体,
被平行于这两个平面的任何一个平面所截,
截面面积都相等,
∴①④这两个几何体的体积一定相等.
故选:D.
点评 本题考查满足祖暅原理的两个几何体的判断,是基础题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
18.已知集合 A={x|-2<x<3},B={x|x≥m}.若 A∩B=∅,则实数m的取值范围是( )
| A. | (-∞,3] | B. | (-2,3] | C. | (-∞,-2) | D. | [3,+∞) |
5.在△ABC中,若b2+c2=a2-bc,则∠A=( )
| A. | 30° | B. | 45° | C. | 60° | D. | 120° |
14.函数y=x 2cosx的导数为( )
| A. | y′=2xcosx-x 2sinx | B. | y′=2xcosx+x 2sinx | ||
| C. | y′=x 2cosx-2xsinx | D. | y′=xcosx-x 2sinx |
15.若双曲线$C:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一条渐近线的倾斜角是直线l:x-2y+1=0倾斜角的两倍,则双曲线的离心率为( )
| A. | $\frac{5}{3}$ | B. | $\frac{{\sqrt{7}}}{3}$ | C. | $\frac{5}{4}$ | D. | $\frac{4}{3}$ |
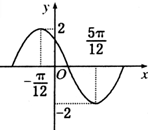 已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)在一个周期内的图象如图所示.
已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)在一个周期内的图象如图所示.