题目内容
14.已知点P(x,y)满足$\left\{\begin{array}{l}{x+y≤4}\\{y≥x}\\{x≥1}\end{array}\right.$,则z=$\frac{y}{x}$的最大值为3.分析 画出满足条件的平面区域,由z=$\frac{y}{x}$表示过平面区域的点(x,y)与(0,0)的直线的斜率,通过图象即可得出.
解答  解:画出满足条件的平面区域,
解:画出满足条件的平面区域,
如图示:
由z=$\frac{y}{x}$表示过平面区域的点(x,y)与(0,0)的直线的斜率,由$\left\{\begin{array}{l}{x=1}\\{x+y=4}\end{array}\right.$,得A(1,3),
显然直线过A(1,3)时,z取得最大值,z=$\frac{y}{x}$=3,
故答案为:3.
点评 本题考查了简单的线性规划问题,利用数形结合判断x,y的取值关系是解决本题的关键.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
5.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上是增函数.令a=f(sin50°),b=f[cos(-50°)],c=f(-tan50°),则( )
| A. | b<a<c | B. | c<b<a | C. | b<c<a | D. | a<b<c |
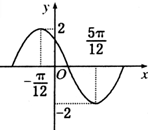 已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)在一个周期内的图象如图所示.
已知函数f(x)=Asin(ωx+ϕ)(A>0,ω>0,|ϕ|<π)在一个周期内的图象如图所示.