题目内容

在平面直角坐标系xOy中，已知点A（
6
5
，0），P（cosα，sinα），其中0≤α≤
π
2
．
（1）若cosα=
5
6
，求证：
PA
⊥
PO
；
（2）若
PA
∥
PO
，求sin（2α+
π
4
）的值．
考点：两角和与差的正弦函数,数量积判断两个平面向量的垂直关系
专题：三角函数的求值
分析：（1）由题意易得点P的坐标，进而可得
PA
和
PO
的坐标，验证其数量积为0即可；
（2）由题意
PA
和
PO
坐标，由
PA
∥
PO
结合角的范围可得α=0，代入计算即可．
解答： 解：（1）∵cosα=
5
6
，0≤α≤
π
2
，
∴sinα=
1-cos2α
=
11
6
，
∴点P的坐标为（
5
6
，
11
6
）．
∴
PA
=（
11
30
，-
11
6
），
PO
=（-
5
6
，-
11
6
）．
∴
PA
•
PO
=
11
30
×（-
5
6
）+（-
11
6
）2=0，
∴
PA
⊥
PO

（2）由题意
PA
=（
6
5
-cosα，-sinα），
PO
=（-cosα，-sinα）．
∵
PA
∥
PO
，∴-sinα•（
6
5
-cosα）-sinαcosα=0，解得sinα=0．
∵0≤α≤
π
2
，∴α=0，∴sin（2α+
π
4
）=sin
π
4
=
2
2
．
点评：本题考查三角函数公式，涉及向量的数量积与垂直关系，属基础题．
练习册系列答案
相关题目
已知函数f（x）=x3-ax2+3x．
（1）若x=3是f（x）的一个极值点，求f（x）在区间[2，a]上的最大值和最小值；
（2）若f（x）在x∈[1，+∞）上单调递增，求实数a的取值范围．
已知函数f（x）=
ax
x2+b
在x=1处取得极值2．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）实数k满足什么条件时，函数f（x）在区间（2k，4k+1）上单调递增？
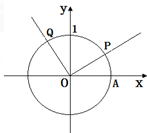设A是单位圆和x轴正半轴的交点，P，Q是单位圆上两点，O是坐标原点，且∠AOP=β，β∈（0，
π
2
），∠AOQ=α，α∈[0，π）．
（1）若点Q的坐标是 （m，
4
5
），其中m＜0，求cos（π-α）+sin（-α）的值．
（2）设P（
3
2
，
1
2
），函数f（α）=sin（α+β），求f（α）的值域．
某志愿者到某山区小学支教，为了解留守儿童的幸福感，该志愿者对某班40名学生进行了一次幸福指数的调查问卷，并用茎叶图表示如下（注：图中幸福指数低于70，说明孩子幸福感弱；幸福指数不低于70，说明孩子幸福感强）．
（Ⅰ）根据茎叶图中的数据完成2×2列联表，并判断能否有95%的把握认为孩子的幸福感强与是否是留守儿童有关？
幸福感强幸福感弱合 计
留守儿童
非留守儿童
合 计
（Ⅱ）从15个留守儿童中按幸福感强弱进行分层抽样，共抽取5人，又在这5人中随机抽取2人进行家访，求这2个学生中恰有一人幸福感强的概率．
参考公式：Χ2=
n(n11n22-n12n21)2
n1+n2+n+1n+2
；  附表：
P（x2≥k）0.0500.010
k3.8416.635
不用计算器计算
（1）（-
27
8
） -
2
3
+（0.002） -
1
2
-10（
5
-2）-1+（
2
-
3
）0
（2）log3
27
+lg25+lg4+7log72+（-9.8）0．
设函数f（x）=lnx+
m
x
，m∈R
（1）当m=e（e为自然对数的底数）时，求f（x）的最小值；
（2）讨论函数g（x）=f′（x）-
x
3
零点的个数；
（3）（理科）若对任意b＞a＞0，
f(b)-f(a)
b-a
＜1恒成立，求m的取值范围．
在雅安发生地震灾害之后，救灾指挥部决定建造一批简易房，供灾区群众临时居住，房形为长方体，高2.5米，前后墙用2.5米高的彩色钢板，两侧用2.5米高的复合钢板，两种钢板的价格都用长度来计算（即钢板的高均为2.5米，用长度乘以单价就是这块钢板的价格），每米单价：彩色钢板为450元，复合钢板为200元，房顶用其他材料建造，每平方米材料费为200元，每套房材料费控制在32000元以内．
（1）设房前面墙的长为x，两侧墙的长为y，一套简易房所用材料费为p，试用x，y表示p；
（2）一套简易房面积S的最大值是多少？当S最大时，前面墙的长度是多少？
已知
3sinα+cosα
3cosα-sinα
=2，则2+3sin（α-3π）sin（
3π
2
-α）-cos2（-α）的值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网