题目内容
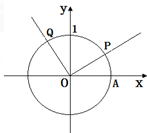 设A是单位圆和x轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且∠AOP=β,β∈(0,
设A是单位圆和x轴正半轴的交点,P,Q是单位圆上两点,O是坐标原点,且∠AOP=β,β∈(0,| π |
| 2 |
(1)若点Q的坐标是 (m,
| 4 |
| 5 |
(2)设P(
| ||
| 2 |
| 1 |
| 2 |
考点:任意角的三角函数的定义,运用诱导公式化简求值
专题:三角函数的求值
分析:(1)利用Q(m,
)在单位圆上,其中m<0,求出m的值,利用诱导公式化简cos(π-α)+sin(-α),然后利用三角函数的定义求解.
(2)利用P(
,
),求出β的值,利用角的范围求出相位的范围,即可通过正弦函数的值域求解函数f(α)=sin(α+β)的值域.
| 4 |
| 5 |
(2)利用P(
| ||
| 2 |
| 1 |
| 2 |
解答:
解:(1)由
,解得m=-
∴m=cosα=-
,sinα=
.…..3分
所以cos(π-α)+sin(-α)=-cosα-sinα=-
.…..6分
(2)由已知P(
,
),∠AOP=β,β∈(0,
),可得β=
,…..8分
因为α∈[0,π),则α+
∈[
,
),所以-
<sin(α+
)≤1.
故f(α)的值域(-
,1].…..12分.
|
| 3 |
| 5 |
∴m=cosα=-
| 3 |
| 5 |
| 4 |
| 5 |
所以cos(π-α)+sin(-α)=-cosα-sinα=-
| 1 |
| 5 |
(2)由已知P(
| ||
| 2 |
| 1 |
| 2 |
| π |
| 2 |
| π |
| 6 |
因为α∈[0,π),则α+
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
故f(α)的值域(-
| 1 |
| 2 |
点评:本题考查三角函数的定义,正弦函数的值域,三角函数的性质以及诱导公式的应用,是中档题.

练习册系列答案
相关题目