题目内容
证明:若a2-b2+2a-4b-3≠0,则a-b≠1.
考点:四种命题间的逆否关系
专题:简易逻辑
分析:原命题不好证明,利用逆否命题的等价性进行证明即可
解答:
证明:若a-b=1,则a2-b2+2a-4b-3=(a+b)(a-b)+2(a-b)-2b-3=(a-b)-1=0成立,
∴根据逆否命题的等价性可知:
若a2-b2+2a-4b-3≠0,则a-b≠1成立.
∴根据逆否命题的等价性可知:
若a2-b2+2a-4b-3≠0,则a-b≠1成立.
点评:本题主要考查命题的证明,利用原命题和逆否命题的等价性转换为证明逆否命题是解决本题的关键.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 函数f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
函数f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<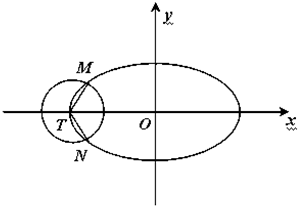 如图,已知椭圆C:
如图,已知椭圆C: