题目内容
17．
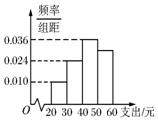学校为了调查学生在课外读物方面的支出情况，抽取了一个容量为n的样本，其频率分布直方图如图，其中支出在[50，60）的同学有30人，若想在这n人中抽取50人，则在[50，60）之间应抽取的人数为（ ）| A． | 10人 | B． | 15人 | C． | 25人 | D． | 30人 |
分析 根据频率直方图的意义，由前三个小组的频率可得样本在[50，60）元的频率，求出样本容量后再计算所求的结果．
解答 解：由题意可知：前三个小组的频率之和为
（0.01+0.024+0.036）×10=0.7，
∴支出在[50，60）元的频率为1-0.7=0.3，
∴n=$\frac{30}{0.3}$=100；
在这100人中抽取50人，在[50，60）之间应抽取的人数为30÷2=15．
故选：B．
点评 本题考查了频率分布直方图的应用问题，是基础题目．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
7．已知$tan（θ+\frac{π}{4}）=\frac{1}{7}$且-$\frac{π}{2}$＜θ＜0，则sinθ=（ ）
| A． | $\frac{4}{5}$ | B． | $\frac{3}{5}$ | C． | $-\frac{3}{5}$ | D． | $-\frac{4}{5}$ |
8．已知{an}是等比数列，a2=2，a5=$\frac{1}{4}$，则a1a2+a2a3+…+anan+1=（ ）
| A． | 16（1-4-n） | B． | 16（1-2-n） | C． | $\frac{32}{3}（1-{4^{-n}}）$ | D． | $\frac{32}{3}（1-{2^{-n}}）$ |
5．已知集合M={x|x2＞4}，N={-3，-2，2，3，4}，则M∩N=（ ）
| A． | {3，4} | B． | {-3，3，4} | C． | {-2，3，4} | D． | {-3，-2，2，3，4} |
12．已知奇函数f（x）满足，x＞0时，f（x）=x2-2x；则x＜0时，f（x）的解析式为（ ）
| A． | -x2-2x | B． | -x2+2x | C． | x2-2x | D． | x2+2x |