题目内容
2.△ABC中,若三个角∠A、∠B、∠C及其所对的边a,b,c均成等差数列,△ABC的面积为4$\sqrt{3}$,且∠B=$\frac{π}{3}$,那么b=4.分析 由a,b,c成等差数列,可得2b=a+c,平方得a2+c2=4b2-2ac,再由△ABC的面积为4$\sqrt{3}$,且∠B=$\frac{π}{3}$,求出ac=16,代入余弦定理cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$求出b的值.
解答 解:∵a,b,c成等差数列,
∴2b=a+c,平方得a2+c2=4b2-2ac.
又△ABC的面积为4$\sqrt{3}$,且∠B=$\frac{π}{3}$,
∴4$\sqrt{3}$=$\frac{1}{2}$•ac•$\frac{\sqrt{3}}{2}$,
∴ac=16.
∴a2+c2=4b2-32.由余弦定理cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{1}{2}$,解得 b=4,
故答案为:4.
点评 解三角形是高考的重要组成部分,不在客观题考查,就在解答题中出现,但一般难度不大.解三角形所涉及的知识点要掌握,如正弦定理、余弦定理、三角形的面积公式等,本题属于中档题.

练习册系列答案
相关题目
10.在△ABC中,a2+c2=b2+$\sqrt{3}$ac.则角B的值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | $\frac{π}{4}$或$\frac{3π}{4}$ |
17.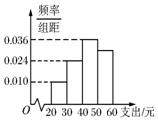 学校为了调查学生在课外读物方面的支出情况,抽取了一个容量为n的样本,其频率分布直方图如图,其中支出在[50,60)的同学有30人,若想在这n人中抽取50人,则在[50,60)之间应抽取的人数为( )
学校为了调查学生在课外读物方面的支出情况,抽取了一个容量为n的样本,其频率分布直方图如图,其中支出在[50,60)的同学有30人,若想在这n人中抽取50人,则在[50,60)之间应抽取的人数为( )
 学校为了调查学生在课外读物方面的支出情况,抽取了一个容量为n的样本,其频率分布直方图如图,其中支出在[50,60)的同学有30人,若想在这n人中抽取50人,则在[50,60)之间应抽取的人数为( )
学校为了调查学生在课外读物方面的支出情况,抽取了一个容量为n的样本,其频率分布直方图如图,其中支出在[50,60)的同学有30人,若想在这n人中抽取50人,则在[50,60)之间应抽取的人数为( )| A. | 10人 | B. | 15人 | C. | 25人 | D. | 30人 |
11.函数 y=(sinx-a)2+1在sinx=1时取得最大值,在sinx=a时取得最小值,则a必满足( )
| A. | [-1,0] | B. | [0,1] | C. | (-∞,-1) | D. | [1,+∞) |