题目内容
6.过点A(1,0)的直线l的倾斜角为$α(0<α<\frac{π}{2})$,直线l绕点A逆时针旋转$\frac{π}{3}$角度得到直线y=1-x.(1)求角α及$cos(\frac{π}{6}-α)$的值;
(2)圆心角为α的扇形周长c为4.求当扇形的面积取最大值时,扇形的半径r及弧长l.
分析 (1)依题意得tan(α+$\frac{π}{3}$)=-1,结合0<α<$\frac{π}{2}$,即可求角α及$cos(\frac{π}{6}-α)$的值;
(2)由c=2r+l=4得l=4-2r(0<r<2),利用扇形的面积公式,结合基本不等式,即可求当扇形的面积取最大值时,扇形的半径r及弧长l.
解答 解:(1)依题意得tan(α+$\frac{π}{3}$)=-1--------------------------------------------------------------------------(2分)
∵0<α<$\frac{π}{2}$,
∴$\frac{π}{3}$<α+$\frac{π}{3}$<$\frac{5π}{6}$,
∴α+$\frac{π}{3}$=$\frac{3π}{4}$,
∴α=$\frac{5π}{12}$-------------------------------------(5分)
由tan(α+$\frac{π}{3}$)=-1得sin(α+$\frac{π}{3}$)=-cos(α+$\frac{π}{3}$)
由sin2(α+$\frac{π}{3}$)+cos2(α+$\frac{π}{3}$)=1得sin(α+$\frac{π}{3}$)=$\frac{\sqrt{2}}{2}$-----------------------------------------(7分)
∴$cos(\frac{π}{6}-α)$=cos[$\frac{π}{2}$-(α+$\frac{π}{3}$)]=sin(α+$\frac{π}{3}$)=$\frac{\sqrt{2}}{2}$--------------------------------------------(8分)
(2)由c=2r+l=4得l=4-2r(0<r<2)------------------------------------(9分)
S=$\frac{1}{2}rl$=r(2-r)≤1,当且仅当r=1时等号成立.------------------(11分)
此时l=αr=$\frac{5π}{12}$----------------------------------------------------------(12分)
点评 本题考查直线的倾斜角,考查扇形的弧长、面积公式,考查学生分析解决问题的能力,属于中档题.

 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案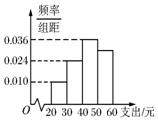 学校为了调查学生在课外读物方面的支出情况,抽取了一个容量为n的样本,其频率分布直方图如图,其中支出在[50,60)的同学有30人,若想在这n人中抽取50人,则在[50,60)之间应抽取的人数为( )
学校为了调查学生在课外读物方面的支出情况,抽取了一个容量为n的样本,其频率分布直方图如图,其中支出在[50,60)的同学有30人,若想在这n人中抽取50人,则在[50,60)之间应抽取的人数为( )| A. | 10人 | B. | 15人 | C. | 25人 | D. | 30人 |
| A. | [-1,0] | B. | [0,1] | C. | (-∞,-1) | D. | [1,+∞) |
| 年龄(岁) | 频率 | |
| 第1组 | [25,30) | 0.1 |
| 第2组 | [30,35) | 0.1 |
| 第3组 | [35,40) | 0.4 |
| 第4组 | [40,45) | 0.3 |
| 第5组 | [45,50] | 0.1 |
(2)从这6人中随机抽取2人担任本次活动的宣传员,求至少有1人年龄在第3组的概率.
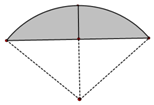 《九章算术》是我国古代数学成就的杰出代表.其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=$\frac{1}{2}$(弦×矢+矢2).弧田由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.
《九章算术》是我国古代数学成就的杰出代表.其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=$\frac{1}{2}$(弦×矢+矢2).弧田由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.