题目内容
8.已知{an}是等比数列,a2=2,a5=$\frac{1}{4}$,则a1a2+a2a3+…+anan+1=( )| A. | 16(1-4-n) | B. | 16(1-2-n) | C. | $\frac{32}{3}(1-{4^{-n}})$ | D. | $\frac{32}{3}(1-{2^{-n}})$ |
分析 先根据a2=2,a5=$\frac{1}{4}$,求出公比q,再根据{anan+1}为等比数列,根据求和公式得到答案.
解答 解:∵{an}是等比数列,a2=2,a5=a2q3=2•q3=$\frac{1}{4}$,
∴则q=$\frac{1}{2}$,a1=4,a1a2=8,
∵$\frac{{a}_{n}{a}_{n+1}}{{a}_{n-1}{a}_{n}}$=q2=$\frac{1}{4}$,
∴数列{anan+1}是以8为首项,$\frac{1}{4}$为公比的等比数列,
∴a1a2+a2a3+a3a4+…+anan+1=$\frac{8[1-(\frac{1}{4})^{n}]}{1-\frac{1}{4}}$=$\frac{32}{3}$(1-4-n).
故选:C.
点评 本题主要考查等比数列的求和问题.属基础题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
19. 执行如图所示的程序框图,若输出的结果为63,则判断框中应填入的条件为( )
执行如图所示的程序框图,若输出的结果为63,则判断框中应填入的条件为( )
 执行如图所示的程序框图,若输出的结果为63,则判断框中应填入的条件为( )
执行如图所示的程序框图,若输出的结果为63,则判断框中应填入的条件为( )| A. | i≤4 | B. | i≤5 | C. | i≤6 | D. | i≤7 |
3.在△ABC中,AB=AC=2,BC•cos(π-A)=1,则cosA的值所在区间是( )
| A. | (-0.5,-0.4) | B. | (-0.4,-0.3) | C. | (0.4,0.6) | D. | (0.8,0.9) |
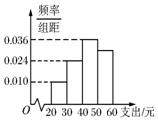 学校为了调查学生在课外读物方面的支出情况,抽取了一个容量为n的样本,其频率分布直方图如图,其中支出在[50,60)的同学有30人,若想在这n人中抽取50人,则在[50,60)之间应抽取的人数为( )
学校为了调查学生在课外读物方面的支出情况,抽取了一个容量为n的样本,其频率分布直方图如图,其中支出在[50,60)的同学有30人,若想在这n人中抽取50人,则在[50,60)之间应抽取的人数为( )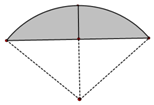 《九章算术》是我国古代数学成就的杰出代表.其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=$\frac{1}{2}$(弦×矢+矢2).弧田由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.
《九章算术》是我国古代数学成就的杰出代表.其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=$\frac{1}{2}$(弦×矢+矢2).弧田由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.