题目内容
9.顶点在单位圆上的△ABC中,角A,B,C所对的边分别为a,b,c.若b2+c2=5,$sinA=\frac{{\sqrt{3}}}{2}$,则S△ABC=$\frac{{\sqrt{3}}}{2}$.分析 由题意和正弦定理求出边a,结合条件和三边关系判断出角A是锐角,由余弦定理求出bc的值,代入三角形面积公式求出S△ABC的值.
解答 解:由题意得,△ABC外接圆的半径是1,
∵$sinA=\frac{\sqrt{3}}{2}$,∴由正弦定理得$\frac{a}{sinA}=2$,则a=$\sqrt{3}$,
∵b2+c2=5,∴b2+c2-a2=3>0,则A是锐角,且A=60°,
由余弦定理得,a2=b2+c2-2bccosA,
则3=5-bc,得bc=2,
∴三角形的面积S△ABC=$\frac{1}{2}bcsinA$=$\frac{{\sqrt{3}}}{2}$,
故答案为:$\frac{{\sqrt{3}}}{2}$.
点评 本题考查了正弦定理、余弦定理,以及三角形面积公式的灵活应用,注意边角关系,属于中档题.

练习册系列答案
相关题目
19. 执行如图所示的程序框图,若输出的结果为63,则判断框中应填入的条件为( )
执行如图所示的程序框图,若输出的结果为63,则判断框中应填入的条件为( )
 执行如图所示的程序框图,若输出的结果为63,则判断框中应填入的条件为( )
执行如图所示的程序框图,若输出的结果为63,则判断框中应填入的条件为( )| A. | i≤4 | B. | i≤5 | C. | i≤6 | D. | i≤7 |
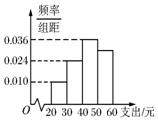 学校为了调查学生在课外读物方面的支出情况,抽取了一个容量为n的样本,其频率分布直方图如图,其中支出在[50,60)的同学有30人,若想在这n人中抽取50人,则在[50,60)之间应抽取的人数为( )
学校为了调查学生在课外读物方面的支出情况,抽取了一个容量为n的样本,其频率分布直方图如图,其中支出在[50,60)的同学有30人,若想在这n人中抽取50人,则在[50,60)之间应抽取的人数为( )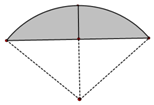 《九章算术》是我国古代数学成就的杰出代表.其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=$\frac{1}{2}$(弦×矢+矢2).弧田由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.
《九章算术》是我国古代数学成就的杰出代表.其中《方田》章给出计算弧田面积所用的经验公式为:弧田面积=$\frac{1}{2}$(弦×矢+矢2).弧田由圆弧和其所对弦所围成,公式中“弦”指圆弧所对弦长,“矢”等于半径长与圆心到弦的距离之差.按照上述经验公式计算所得弧田面积与其实际面积之间存在误差.