题目内容
7.已知$tan(θ+\frac{π}{4})=\frac{1}{7}$且-$\frac{π}{2}$<θ<0,则sinθ=( )| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $-\frac{3}{5}$ | D. | $-\frac{4}{5}$ |
分析 由条件利用两角和与差的正切、同角三角函数的基本关系,求得sinθ的值.
解答 解:∵$tan(θ+\frac{π}{4})=\frac{1}{7}$,
∴$\frac{tanθ+tan\frac{π}{4}}{1-tanθtan\frac{π}{4}}$=$\frac{tanθ+1}{1-tanθ}$=$\frac{1}{7}$,则tanθ=-$\frac{3}{4}$.
∴$\frac{sinθ}{cosθ}$=-$\frac{3}{4}$.
又∵-$\frac{π}{2}$<θ<0,sin2θ+cos2θ=1,
∴sinθ=-$\frac{3}{5}$.
故选:C.
点评 本题主要考查同角三角函数的基本关系,属于基础题.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
2.已知函数f(x)=$\left\{\begin{array}{l}{\sqrt{x},x>1}\\{{2}^{|x|},x≤1}\end{array}\right.$,函数g(x)=f(x)-k有3个零点,则实数k的取值范围为( )
| A. | (0,+∞) | B. | [1,+∞) | C. | (0,2) | D. | (1,2] |
19. 执行如图所示的程序框图,若输出的结果为63,则判断框中应填入的条件为( )
执行如图所示的程序框图,若输出的结果为63,则判断框中应填入的条件为( )
 执行如图所示的程序框图,若输出的结果为63,则判断框中应填入的条件为( )
执行如图所示的程序框图,若输出的结果为63,则判断框中应填入的条件为( )| A. | i≤4 | B. | i≤5 | C. | i≤6 | D. | i≤7 |
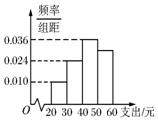 学校为了调查学生在课外读物方面的支出情况,抽取了一个容量为n的样本,其频率分布直方图如图,其中支出在[50,60)的同学有30人,若想在这n人中抽取50人,则在[50,60)之间应抽取的人数为( )
学校为了调查学生在课外读物方面的支出情况,抽取了一个容量为n的样本,其频率分布直方图如图,其中支出在[50,60)的同学有30人,若想在这n人中抽取50人,则在[50,60)之间应抽取的人数为( )