题目内容

12．已知奇函数f（x）满足，x＞0时，f（x）=x2-2x；则x＜0时，f（x）的解析式为（　　）
A．-x2-2xB．-x2+2xC．x2-2xD．x2+2x

分析 已知x＞0时的解析式，所以求x＜0时的解析式可取-x，以便利用条件，然后结合奇函数定义即可解决问题．

解答 解：设x＜0，则-x＞0，
因为x≥0时，f（x）=x2-2x，
所以f（-x）=x2+2x，（x＜0），
又f（x）为奇函数，即f（-x）=-f（x），
所以-f（x）=x2+2x，即f（x）=-x2-2x，（x＜0）．
故选A．

点评 本题考查了借助函数的奇偶性求解函数的解析式，属于基础题．

练习册系列答案
相关题目
2．已知函数f（x）=$\left\{\begin{array}{l}{\sqrt{x}，x＞1}\\{{2}^{|x|}，x≤1}\end{array}\right.$，函数g（x）=f（x）-k有3个零点，则实数k的取值范围为（　　）
A．（0，+∞）B．[1，+∞）C．（0，2）D．（1，2]
3．在△ABC中，AB=AC=2，BC•cos（π-A）=1，则cosA的值所在区间是（　　）
A．（-0.5，-0.4）B．（-0.4，-0.3）C．（0.4，0.6）D．（0.8，0.9）
20．已知函数f（x）=lnx+ax2
（1）讨论f（x）的单调性；
（2）设a＞1，若对任意x1，x2∈（0，+∞），恒有|f（x1）-f（x2）|≥4|x1-x2|，求a的取值范围．
7．已知集合M={x|（x+2）（x-2）＞0}，N={-3，-2，2，3，4}，则M∩N=（　　）
A．{3，4}B．{-3，3，4}C．{-2，3，4}D．{-3，-2，2，3，4}
17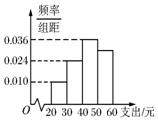．学校为了调查学生在课外读物方面的支出情况，抽取了一个容量为n的样本，其频率分布直方图如图，其中支出在[50，60）的同学有30人，若想在这n人中抽取50人，则在[50，60）之间应抽取的人数为（　　）
A．10人B．15人C．25人D．30人
4．已知定义在R上的函数f（x）满足f（x）•f（x+2）=13，若f（-1）=2，则f（2013）=$\frac{13}{2}$．
1．已知tanα=2且$π＜α＜\frac{3π}{2}$，则sinα的值是-$\frac{2\sqrt{5}}{5}$．
2．f（x）是定义在（-2，2）上的减函数，若f （m-1）＞f（2m-1），则实数m的取值范围是（　　）
A．（0，+∞）B．（0，$\frac{3}{2}$）C．（-1，3）D．（$-\frac{1}{2}$，$\frac{3}{2}$）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网