题目内容
15.已知双曲线:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1,(a>0,b>0)的左、右焦点分别为F1,F2,焦距为2c,直线y=$\sqrt{3}$(x+c)与双曲线的一个交点M满足∠MF1F2=2∠MF2F1,则双曲线的离心率为1$+\sqrt{3}$.分析 由已知直线过左焦点F1,且其倾斜角为60°,∠MF1F2=2∠MF2F1,可得∠MF1F2=60°,∠MF2F1=30°,即F1M⊥F2M,运用直角三角形的性质和双曲线的定义,由离心率公式计算即可得到所求值.
解答  解:∵直线y=$\sqrt{3}$(x+c)过左焦点F1,且其倾斜角为60°,
解:∵直线y=$\sqrt{3}$(x+c)过左焦点F1,且其倾斜角为60°,
∠MF1F2=2∠MF2F1,
∴∠MF1F2=60°,∠MF2F1=30°.
∴∠F1MF2=90°,即F1M⊥F2M.
∴|MF1|=$\frac{1}{2}$|F1F2|=c,|MF2|=|F1F2|sin600=$\sqrt{3}$c,
由双曲线的定义有:|MF2|-|MF1|=$\sqrt{3}$c-c=2a,
∴离心率e=$\frac{c}{a}$=$\frac{2}{\sqrt{3}-1}$=$\sqrt{3}$+1.
故答案为:1$+\sqrt{3}$.
点评 本题考查双曲线的离心率的求法,注意运用双曲线的定义和直角三角形的锐角三角函数的定义,考查运算能力,属于中档题.

练习册系列答案
相关题目
6.已知函数$f(x)=\left\{\begin{array}{l}{2^x}-2,x≥0\\{log_{\frac{1}{2}}}({-x}),x<0\end{array}\right.$,若f[f(m)]<0,则实数m的取值范围为( )
| A. | $({-3,-1}]∪({-\frac{1}{2},1}]∪({2,+∞})$ | B. | $({-∞,-2}]∪({-1,-\frac{1}{2}}]∪({1,{{log}_2}3})$ | ||
| C. | $({-∞,-1}]∪({0,\frac{1}{2}}]∪({1,+∞})$ | D. | (-∞,-3]∪(-1,0]∪(1,log23) |
10.已知某几何体的三视图如图表 所示,则该几何体的体积为( )


| A. | $\frac{16}{3}$ | B. | $\frac{64}{3}$ | C. | $\frac{80}{3}$ | D. | $\frac{43}{3}$ |
7.若正数a,b满足3+log2a=2+log3b=log6(a+b),则$\frac{1}{a}+\frac{1}{b}$等于( )
| A. | 18 | B. | 36 | C. | 72 | D. | 144 |
5.“x<2”是“x2<4”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
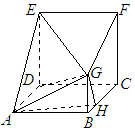 在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH
在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a正方形,CF⊥平面ABCD,BG⊥平面ABCD,且AB=2BG=4BH