题目内容
复数z=
（i为虚数单位且a＜0）在复平面内对应的点位于（ ）
| 3-ai |
| i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点：复数的代数表示法及其几何意义,复数代数形式的乘除运算
专题：
分析：直接由复数代数形式的除法运算化简，求出复数z对应点的坐标，则答案可求．
解答：
解：∵z=
=
=-a-3i，
∴复数z=
（i为虚数单位且a＜0）在复平面内对应的点的坐标为（-a，-3），
∵a＜0，
∴-a＞0．
∴点（-a，-3）位于第四象限．
故选：D．
| 3-ai |
| i |
| (3-ai)(-i) |
| -i2 |
∴复数z=
| 3-ai |
| i |
∵a＜0，
∴-a＞0．
∴点（-a，-3）位于第四象限．
故选：D．
点评：本题考查了复数代数形式的除法运算，考查了复数的代数表示法及其几何意义，是基础题．
练习册系列答案
口算题天天练系列答案
相关题目
设i为虚数单位，复数
在复平面上对应的点在（ ）
| 2+i |
| i2 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知曲线y=cosx，其中x∈[0，
π]，则该曲线与坐标轴围成的面积等于（ ）
| 3 |
| 2 |
| A、1 | ||
| B、2 | ||
C、
| ||
| D、3 |
二次函数y=ax2+bx与指数函数y=（-
）x的图象只可能是（ ）
| b |
| a |
A、 |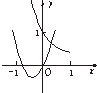
B、 |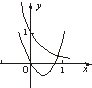
C、 |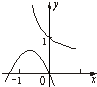
D、 |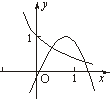
设α，β为锐角，那么“sin2α+sin2β=sin（α+β）”是“α+β=
”的（ ）
| π |
| 2 |
| A、充分非必要条件 |
| B、必要非充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
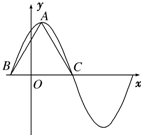已知f（x）=6cos2