题目内容
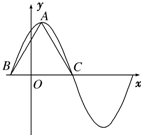已知f（x）=6cos2| ωx |
| 2 |
| 3 |
（Ⅰ）求ω的值；
（Ⅱ）当x∈[0，2]时，求函数f（x）的值域；
（Ⅲ）若f（x0）=
6
| ||
| 5 |
| 10 |
| 3 |
| 2 |
| 3 |
考点：由y=Asin（ωx+φ）的部分图象确定其解析式,正弦函数的图象,函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：（Ⅰ）利用二倍角的余弦公式降幂后化积，由△ABC为正三角形求得函数的半周期，从而求得周期，则ω的值可求；
（Ⅱ）直接由x的范围求函数的值域；
（Ⅲ）由f（x0）=
，结合（Ⅰ）求得sin（
+
）=
，再结合x0∈（-
，
）求得cos（
+
），写出f（x0-1）后展开两角差的正弦得答案．
（Ⅱ）直接由x的范围求函数的值域；
（Ⅲ）由f（x0）=
6
| ||
| 5 |
| πx0 |
| 4 |
| π |
| 3 |
| 3 |
| 5 |
| 10 |
| 3 |
| 2 |
| 3 |
| πx0 |
| 4 |
| π |
| 3 |
解答：
解：（Ⅰ）由f（x）=6cos2
+
sinωx-3，得：
f（x）=3cosωx+
sinωx=2
sin（ωx+
）．
又正三角形ABC的高为2
，从而BC=4．
∴函数f（x）的周期T=4×2=8，即
=8，ω=
；
（Ⅱ）由（Ⅰ）得，f（x）=2
sin（
x+
）．
当x∈[0，2]时，
x+
∈[
，
]，
∴2
sin(
x+
)∈[
，2
]；
（Ⅲ）∵f（x0）=
，
由（1）有f（x0）=2
sin（
+
）=
，
即sin（
+
）=
．
由x0∈（-
，
），
知
+
∈（-
，
），
∴cos（
+
）=
=
．
故f（x0-1）=2
sin(
x0-
+
)
=2
sin[(
x0+
)-
]
=2
×(
×
-
×
)
=-
．
| ωx |
| 2 |
| 3 |
f（x）=3cosωx+
| 3 |
| 3 |
| π |
| 3 |
又正三角形ABC的高为2
| 3 |
∴函数f（x）的周期T=4×2=8，即
| 2π |
| ω |
| π |
| 4 |
（Ⅱ）由（Ⅰ）得，f（x）=2
| 3 |
| π |
| 4 |
| π |
| 3 |
当x∈[0，2]时，
| π |
| 4 |
| π |
| 3 |
| π |
| 3 |
| 5π |
| 6 |
∴2
| 3 |
| π |
| 4 |
| π |
| 3 |
| 3 |
| 3 |
（Ⅲ）∵f（x0）=
6
| ||
| 5 |
由（1）有f（x0）=2
| 3 |
| πx0 |
| 4 |
| π |
| 3 |
6
| ||
| 5 |
即sin（
| πx0 |
| 4 |
| π |
| 3 |
| 3 |
| 5 |
由x0∈（-
| 10 |
| 3 |
| 2 |
| 3 |
知
| πx0 |
| 4 |
| π |
| 3 |
| π |
| 2 |
| π |
| 2 |
∴cos（
| πx0 |
| 4 |
| π |
| 3 |
1-(
|
| 4 |
| 5 |
故f（x0-1）=2
| 3 |
| π |
| 4 |
| π |
| 4 |
| π |
| 3 |
=2
| 3 |
| π |
| 4 |
| π |
| 3 |
| π |
| 4 |
=2
| 3 |
| 3 |
| 5 |
| ||
| 2 |
| 4 |
| 5 |
| ||
| 2 |
=-
| ||
| 5 |
点评：本题考查了y=Asin（ωx+φ）的图象，考查了三角函数值得求法，考查了两角和与差的三角函数，解答此体的关键是拆角和配角，是中档题．
练习册系列答案
一本好题口算题卡系列答案
相关题目
复数z=
（i为虚数单位且a＜0）在复平面内对应的点位于（ ）
| 3-ai |
| i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
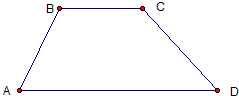如图，已知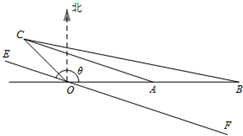
如图，O为总信号源点，A，B，C是三个居民区，已知A，B都在O的正东方向上，OA=10km，OB=20km，C在O的北偏西45°方向上，CO=5