题目内容
17.已知正数a,b,c满足b+c≥a,则$\frac{b}{c}$+$\frac{c}{a+b}$的最小值为$\sqrt{2}$-$\frac{1}{2}$.分析 由题意变形可得$\frac{b}{c}$+$\frac{c}{a+b}$≥$\frac{b}{c}$+$\frac{c}{2b+c}$=($\frac{b}{c}$+$\frac{1}{2}$)+$\frac{c}{2b+c}$-$\frac{1}{2}$=$\frac{2b+c}{2c}$+$\frac{c}{2b+c}$-$\frac{1}{2}$,由基本不等式可得.
解答 解:∵正数a,b,c满足b+c≥a,
∴$\frac{b}{c}$+$\frac{c}{a+b}$≥$\frac{b}{c}$+$\frac{c}{2b+c}$=($\frac{b}{c}$+$\frac{1}{2}$)+$\frac{c}{2b+c}$-$\frac{1}{2}$
=$\frac{2b+c}{2c}$+$\frac{c}{2b+c}$-$\frac{1}{2}$≥$\sqrt{2}$-$\frac{1}{2}$
当且仅当$\frac{2b+c}{2c}$=$\frac{c}{2b+c}$时取等号.
故答案为:$\sqrt{2}$-$\frac{1}{2}$
点评 本题考查基本不等式求式子的最值,凑出可用基本不等式的形式是解决问题的关键,属中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.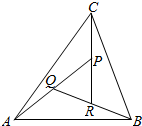 如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点为P,若$\overrightarrow{AP}=m\vec a+n\vec b$,则m、n对应的值为 ( )
如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点为P,若$\overrightarrow{AP}=m\vec a+n\vec b$,则m、n对应的值为 ( )
 如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点为P,若$\overrightarrow{AP}=m\vec a+n\vec b$,则m、n对应的值为 ( )
如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}=\overrightarrow b$,AP的中点为Q,BQ的中点为R,CR的中点为P,若$\overrightarrow{AP}=m\vec a+n\vec b$,则m、n对应的值为 ( )| A. | $\frac{2}{7},\frac{4}{7}$ | B. | $\frac{1}{2},\frac{1}{4}$ | C. | $\frac{1}{6},\frac{2}{7}$ | D. | $\frac{1}{6},\frac{3}{7}$ |
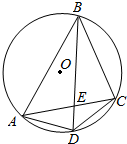 如图,⊙O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于点E.
如图,⊙O是△ABC的外接圆,D是$\widehat{AC}$的中点,BD交AC于点E.