题目内容
12．对于两个非零向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{a}$∥$\overrightarrow{b}$是＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=0的必要不充分条件（填充分不必要、必要不充分、充要、既不充分又不必要）条件．分析 根据充分条件和必要条件的定义结合向量夹角与向量平行的关系进行求解即可．
解答 解：若$\overrightarrow{a}$∥$\overrightarrow{b}$，则＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=0或＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=π，则充分性不成立，
若＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=0，则$\overrightarrow{a}$∥$\overrightarrow{b}$成立，即必要性成立，
故$\overrightarrow{a}$∥$\overrightarrow{b}$是＜$\overrightarrow{a}$，$\overrightarrow{b}$＞=0的必要不充分条件，
故答案为：必要不充分条件
点评 本题主要考查充分条件和必要条件的判断，利用向量平行的定义是解决本题的关键．
练习册系列答案
相关题目
19．已知抛物线C：x2=2y的焦点为F，P为抛物线C上任意一点，点M（-2，4m-2m+4），m∈R，则|MP|+|PF|的最小值为（ ）
| A． | $\frac{5}{2}$ | B． | $\frac{13}{4}$ | C． | $\frac{9}{2}$ | D． | $\frac{17}{4}$ |
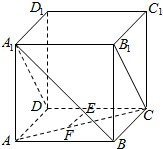如图，正方体ABCD-A1B1C1D1中，E是A1B上的点，F是AC上的点，且A1E=2EB，CF=2AF．求证：EF∥平面A1B1CD．