题目内容

2．一块石材表示的几何体的三视图如图所示，将该石材切削、打磨，加工成球，则能得到的最大球的半径等于2．

分析 由题意，该几何体为三棱柱，所以最大球的半径为正视图直角三角形内切圆的半径r．

解答 解：由题意，该几何体为三棱柱，所以最大球的半径为正视图直角三角形内切圆的半径r，
则8-r+6-r=10，
∴r=2．
故答案为：2．

点评 本题考查三视图，考查几何体的内切圆，考查学生的计算能力，属于基础题．

练习册系列答案
相关题目
7．用列举法表示A={x|-4＜x＜2，x∈Z}．
13．已知函数f（x）=$\left\{\begin{array}{l}{e^x+a，x≤0}\\{3x-1，x＞0}\end{array}\right.$（a∈R），若函数f（x）在R上有两个零点，则a的取值范围是（　　）
A．（-∞，-1）B．（-∞，0）C．（-1，0）D．[-1，0）
10．已知圆F1：（x+1）2+y2=1，圆F2：（x-1）2+y2=25，动圆P与圆F1外切并且与圆F2内切，动圆圆心P的轨迹为曲线C．
（Ⅰ）求曲线C的方程；
（Ⅱ）若曲线C与x轴的交点为A1，A2，点M是曲线C上异于点A1，A2的点，直线A1M与A2M的斜率分别为k1，k2，求k1k2的值．
（Ⅲ）过点（2，0）作直线l与曲线C交于A，B两点，在曲线C上是否存在点N，使$\overrightarrow{OA}$+$\overrightarrow{OB}$=$\overrightarrow{ON}$？若存在，请求出直线l的方程；若不存在，请说明理由．
17．已知复数z1=3-i，z2=1+i，$\overline{{z}_{1}}$是z1的共轭复数，则$\frac{\overline{{z}_{1}}}{{z}_{2}}$=（　　）
A．1+iB．1-iC．2+iD．2-i
7．已知$U=\{y|y={2^x}，x≥-1\}，A=\{x|\frac{1}{x-1}≥1\}$，则∁UA=（　　）
A．$[\frac{1}{2}，2]$B．[2，+∞）C．$[\frac{1}{2}，1]∪（2，+∞）$D．$[\frac{1}{2}，2）∪（2，+∞）$
14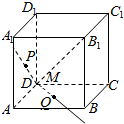．如图，M是正方体ABCD-A1B1C1D1对角线AC1上的动点，过点M作垂直于面ACC1A1的直线与正方体表面分别交于P、Q两点，设AM=x，PQ=y，则函数y=f（x）的图象大致为（　　）
A．B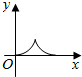．C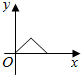．D．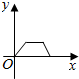
11．设α、β为两个不同平面，若直线l在平面α内，则“α⊥β”是“l⊥β”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
12．已知f（x）定义域为A，值域为B．若B?A，则称f（x）在A上为“内向函数”，若A?B，则称f（x）在A上为“外向函数”．
（1）若f（x）=tanx，试判断f（x）在定义域上是“内向函数”还是“外向函数”；
（2）若$f（x）=lnx-\frac{a}{x}（{a≤0}）$在[1，e]上是“内向函数”，求a的范围；
（3）若B⊆A，则称f（x）在A上为“伪内向函数”．试证：f（x）=ax-lnx在[1，+∞）上是“伪内向函数”的充要条件是a≥1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网