题目内容
7．已知$U=\{y|y={2^x}，x≥-1\}，A=\{x|\frac{1}{x-1}≥1\}$，则∁UA=（ ）| A． | $[\frac{1}{2}，2]$ | B． | [2，+∞） | C． | $[\frac{1}{2}，1]∪（2，+∞）$ | D． | $[\frac{1}{2}，2）∪（2，+∞）$ |
分析 化简集合A，U，再根据补集的定义求得∁UA．
解答 解：U={y|y=2x，x≥-1}=[$\frac{1}{2}$，+∞），
∵$\frac{1}{x-1}$≥1，
∴$\frac{2-x}{x-1}$≥0，
∴1＜x≤2，
∴A=（1，2]，
∴∁UA=[$\frac{1}{2}$，1]∪（2，+∞）
故选：C．
点评 本题主要考查补集的定义和求法，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
一块石材表示的几何体的三视图如图所示，将该石材切削、打磨，加工成球，则能得到的最大球的半径等于2．
12．已知点A（1，1），B（2，1），C（1，2），若-1≤λ≤2，2≤μ≤3，则$|{λ\overrightarrow{AB}+μ\overrightarrow{AC}}|$的取值范围是（ ）
| A． | [1，10] | B． | $[{\sqrt{5}，\sqrt{13}}]$ | C． | [1，5] | D． | $[{2，\sqrt{13}}]$ |
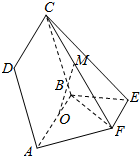如图所示，点E，F在以AB为直径的圆O（O为圆心）上，AB∥EF，平面ABCD⊥平面ABEF，且AB=2，AD=EF=1