题目内容
11.设α、β为两个不同平面,若直线l在平面α内,则“α⊥β”是“l⊥β”的( )| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 根据充分条件和必要条件的定义结合面面垂直的判定定理进行判断即可.
解答 解:面面平行的判定定理:一个平面过另一个平面的垂线,则这两个平面垂直.
因为直线l?α,且l⊥β
所以由判断定理得α⊥β.
所以直线l?α,且l⊥β⇒α⊥β
若α⊥β,直线l?α则直线l⊥β,或直线l∥β,或直线l与平面β相交,或直线l在平面β内.
所以“α⊥β”是“l⊥β”的必要不充分条件.
故选:B.
点评 本题主要考查充分条件和必要条件的判断,利用空间面面垂直的判定定理和性质定理是解决本题的关键.

练习册系列答案
相关题目
16.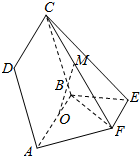 如图所示,点E,F在以AB为直径的圆O(O为圆心)上,AB∥EF,平面ABCD⊥平面ABEF,且AB=2,AD=EF=1
如图所示,点E,F在以AB为直径的圆O(O为圆心)上,AB∥EF,平面ABCD⊥平面ABEF,且AB=2,AD=EF=1
(Ⅰ)设FC的中点为M,求证:OM∥面DAF;
(Ⅱ)求证:AF⊥面CBF.
 如图所示,点E,F在以AB为直径的圆O(O为圆心)上,AB∥EF,平面ABCD⊥平面ABEF,且AB=2,AD=EF=1
如图所示,点E,F在以AB为直径的圆O(O为圆心)上,AB∥EF,平面ABCD⊥平面ABEF,且AB=2,AD=EF=1(Ⅰ)设FC的中点为M,求证:OM∥面DAF;
(Ⅱ)求证:AF⊥面CBF.
1.已知数列${a_n}=n•sin\frac{nπ}{2}$,则a1+a2+a3+…+a100=( )
| A. | -48 | B. | -50 | C. | -52 | D. | -49 |
 一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的半径等于2.
一块石材表示的几何体的三视图如图所示,将该石材切削、打磨,加工成球,则能得到的最大球的半径等于2.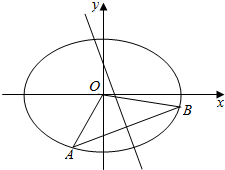 已知椭圆$\frac{{x}^{2}}{2}$+y2=1上两个不同的点A,B关于直线$y=mx+\frac{1}{2}(m≠0)$对称.
已知椭圆$\frac{{x}^{2}}{2}$+y2=1上两个不同的点A,B关于直线$y=mx+\frac{1}{2}(m≠0)$对称.